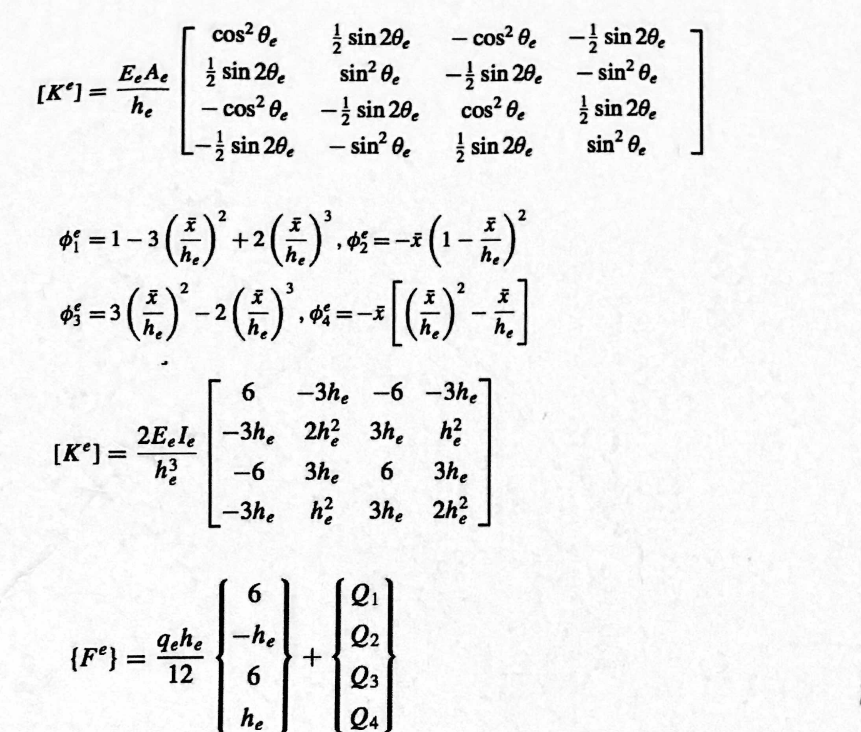
. (20 points) In an Eulelr-Bernoulli beam element which spans, in local coordinates, from x = 0 to x = he, the element properties are given as: E is constant, and I(x) = 1 + 2x Starting with the general formula for Ke, that we derived in class, derive (i.e., not just state) the K23 element of the stiffness matrix for this element. cos e sin 20 -cos e sin 20 E.A. sin 20 sin e - sin 20 - sin e [Ke] = he - cos -sin 20 cos Be sin 20 sin 20. -sin 0. sin 20 sin e 3 1-3 (A)+2(A)--(1-2) = 1 3 =1-3 =3 X h. he he = [(A) - A ] 6 -3he -6 -3he 2Eele -3he 2h2 3h, h2 [Ke] = h -6 3he 6 3he -3he h 3he 2h2 6 Q1 {Fe} = gehe -he Q2 + 12 6 23 he Q4