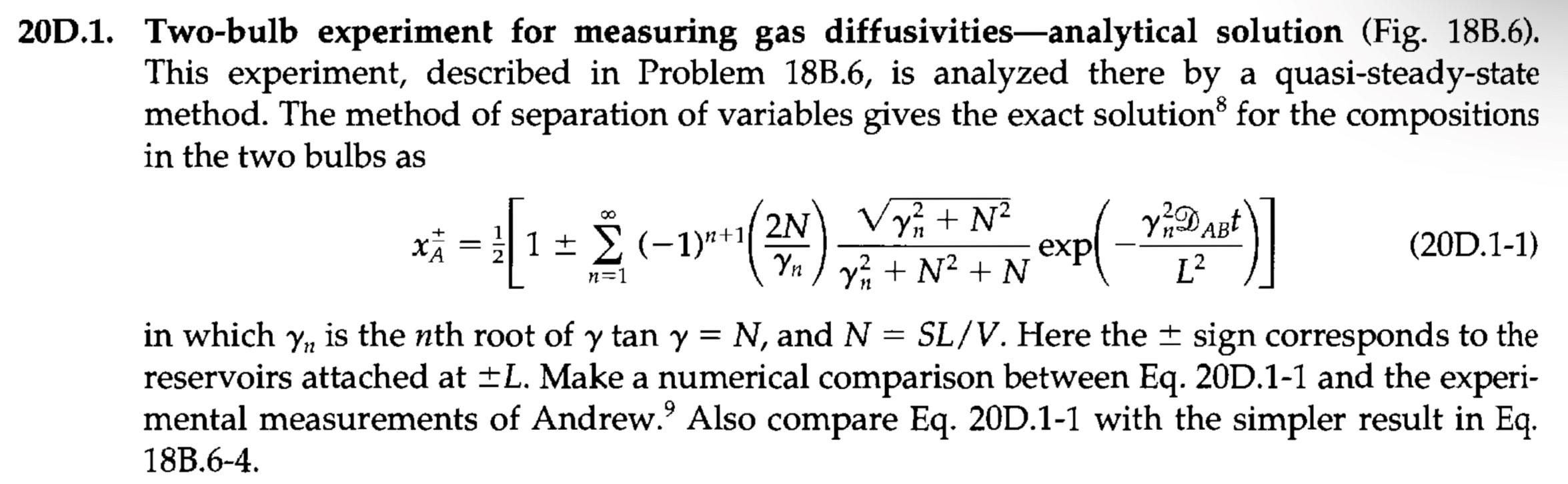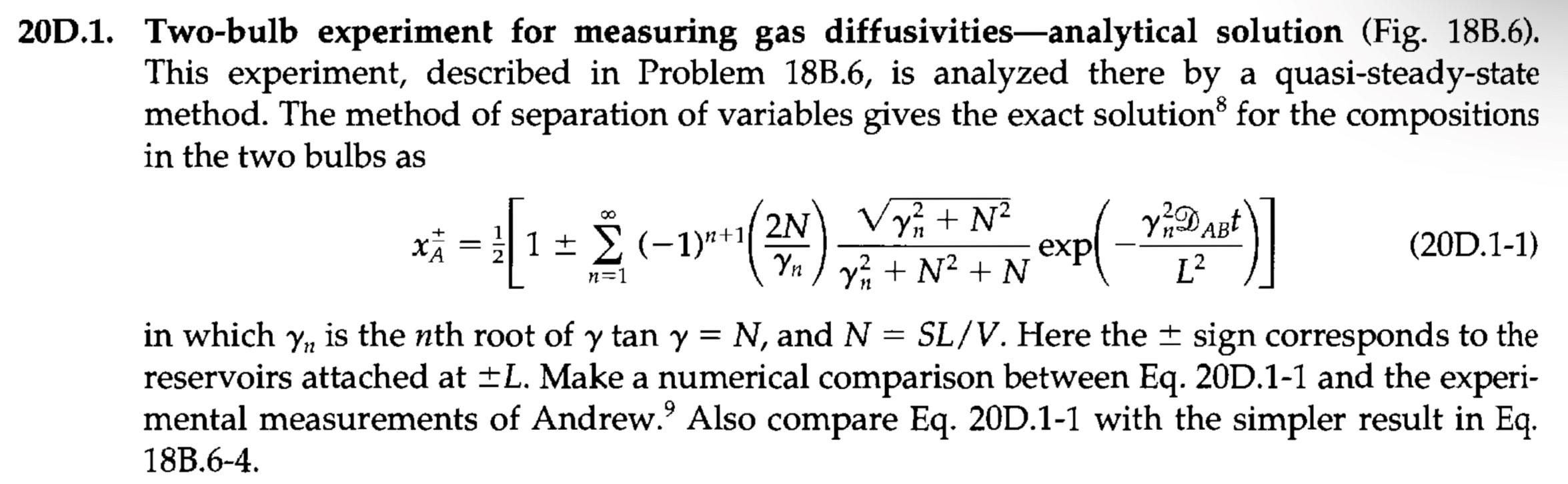
20D.1. Two-bulb experiment for measuring gas diffusivitiesanalytical solution (Fig. 18B.6). This experiment, described in Problem 18B.6, is analyzed there by a quasi-steady-state method. The method of separation of variables gives the exact solution for the compositions in the two bulbs as 2N Vy n + N2 x 7 X + (-1)^+11 exp (20D.1-1) Yn ) y + N2 + N in which yn is the nth root of y tan y = N, and N = y SL/V. Here the + sign corresponds to the reservoirs attached at +L. Make a numerical comparison between Eq. 20D.1-1 and the experi- mental measurements of Andrew. Also compare Eq. 20D.1-1 with the simpler result in Eq. 18B.6-4. - [= 1 ( 2D ABE n=1 L2 - Stopcock Fig. 18B.6. Sketch of a two- bulb apparatus for measuring gas diffusivities. The stirrers in the two bulbs maintain uni- form concentration in the bulbs. z = -L z = 0 z = L Volume V Volume V Entire gaseous Mole fraction of A in left bulb is x = 1 - ** Mole fraction of A in right bulb is x (t) system is at constant p and T 18B.6. Two-bulb experiment for measuring gas diffusivity-quasi-steady-state analysis (Fig. 18B.6). One way of measuring gas diffusivities is by means of a two-bulb experiment. The left bulb and the tube from z = -L to z = 0 are filled with gas A. The right bulb and the tube from z = 0 to z= +L are filled with gas B. At time t = 0 the stopcock is opened, and diffusion begins; then the concentrations of A in the two well-stirred bulbs change. One measures xas a function of time, and from this deduces D AB. We wish to derive the equations describing the diffusion. Since the bulbs are large compared with the tube, x, and x change very slowly with time. Hence the diffusion in the tube can be treated as a quasi-steady-state problem, with the boundary conditions that XA = x, and z = -L, and that X A = x, at z = +L. (a) Write a molar balance on A over a segment Az of the tube (of cross-sectional area S), and show that NAz = C, a constant. (b) Show that Eq. 18.0-1 simplifies, for this problem, to dxA NAz = - DAB (18B.6-1) dz (c) Integrate this equation, using (a). Call the constant of integration Cz. (d) Evaluate the constant by requiring that XA = x4 at z = +L. (e) Next set xa = XA (or 1 - **) at z = -L, and solve for NAz to get finally AB NAz = (-x) (18B.6-2) L (f) Make a mass balance on substance A over the right bulb to obtain CD dx SC - **) = Vc L dt AB (18B.6-3) (g) Integrate the equation in (f) to get an expression for x, which contains DAB: SD AB In (183.6-4) LV (h) Suggest a method of plotting the experimental data to evaluate DAB