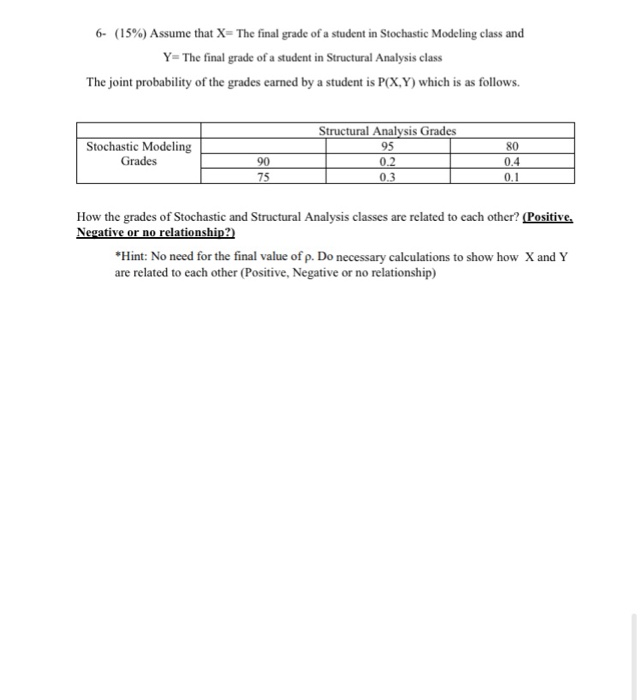
Question
21. A random sample of size n = 250 yields 80 successes. Calculate the 95% confidence interval for p. 22. A random sample of size
21. A random sample of size n = 250 yields 80
successes. Calculate the 95% confidence interval for p.
22. A random sample of size n = 452 yields 113
successes. Calculate the 95% confidence interval for p.
23. George enjoys throwing horse shoes. Last week
he tossed 150 shoes and obtained 36 ringers.
(Ringers are good.) Next week he plans to
throw 250 shoes. Assume that George's tosses
satisfy the assumptions of Bernoulli trials.
(a) Calculate the point prediction of the number of ringers that George will obtain next
week.
(b) Calculate the 90% prediction interval for
the number of ringers George will obtain
next week.
(c) It turns out that next week George obtains
62 ringers. Given this information, comment on your answers in parts (a) and (b)
1. A full house in poker is a hand where three cards share one rank and two cards share
another rank. How many ways are there to get a full-house? What is the probability of
getting a full-house?
2. 20 politicians are having a tea party, 6 Democrats and 14 Republicans. To prepare,
they need to choose:
3 people to set the table, 2 people to boil the water, 6 people to make the scones.
Each person can only do 1 task. (Note that this doesn't add up to 20. The rest of the
people don't help.)
(a) In how many different ways can they choose which people perform these tasks?
(b) Suppose that the Democrats all hate tea. If they only give tea to 10 of the 20 people,
what is the probability that they only give tea to Republicans?
(c) If they only give tea to 10 of the 20 people, what is the probability that they give tea
to 9 Republicans and 1 Democrat?
3. Let C and D be two events with P(C) = 0.25, P(D) = 0.45, and P(C ? D) = 0.1.
What is P(Cc ? D)?
4. More cards! Suppose you want to divide a 52 card deck into four hands with 13 cards
each. What is the probability that each hand has a king?
5. Corrupted by their power, the judges running the popular game show America's Next
Top Mathematician have been taking bribes from many of the contestants. Each episode,
a given contestant is either allowed to stay on the show or is kicked off.
If the contestant has been bribing the judges she will be allowed to stay with probability 1.
If the contestant has not been bribing the judges, she will be allowed to stay with probability
1/3.
Suppose that 1/4 of the contestants have been bribing the judges. The same contestants
bribe the judges in both rounds, i.e., if a contestant bribes them in the first round, she
bribes them in the second round too (and vice versa).
(a) If you pick a random contestant who was allowed to stay during the first episode, what
is the probability that she was bribing the judges?
(b) If you pick a random contestant, what is the probability that she is allowed to stay
during both of the first two episodes?
(c) If you pick random contestant who was allowed to stay during the first episode, what
is the probability that she gets kicked off during the second episode?
6. There is a screening test for prostate cancer that looks at the level of PSA (prostatespecific antigen) in the blood. There are a number of reasons besides prostate cancer that
a man can have elevated PSA levels. In addition, many types of prostate cancer develop
so slowly that that they are never a problem. Unfortunately there is currently no test



Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


