2^50; n^0.5; 1; 8^(log n); 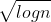; 1.05^n; 4n^3/2; log log n; 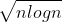; 5000n + 25 log n

a. Arrange them in increasing order of growth rate. In Computer Science, the following terms are used informally.2. We say that a function f(n) is - a constant if f(n) is O(1), - logarithmic if f(n) is O(logk n) for some constant k 1, - polynomial if f(n) is O(nk) for some constant k 1, - exponential if f(n) is (an) for some constant a > 1. When classifying a function f(n), go through the list sequentially. That is, first check if f(n) is a constant function. If yes, youre done; otherwise check if f(n) is logarithmic. If yes, youre done; otherwise, check if f(n) is polynomial. If yes, youre done; otherwise, check if it is exponential. b. Classify the ten functions on whether they are a constant function, logarithmic, polynomial or exponential.

Vlogn Vnlogn