
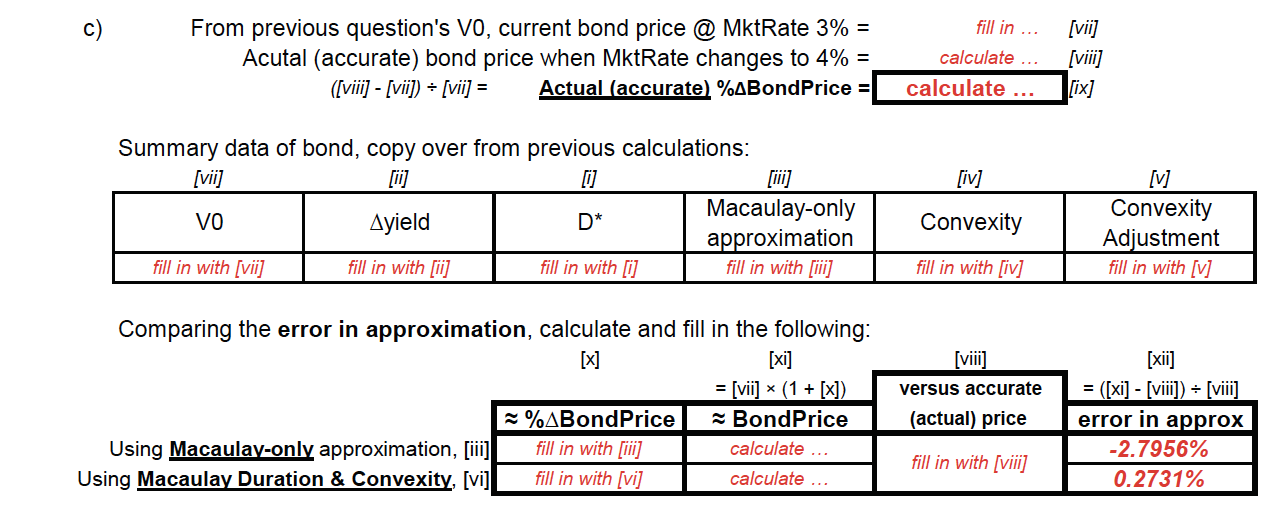
27. Continuing from previous question, use Modified Duration and Convexity to approximate the percentage change in price of the bond when its market rate change from 3% to 4%. PS: to save time, calculated for you, use a Macaulay Duration D of 19.9855. a) The "first order approximation" of %ABondPrice is a linear approximation. It uses Modified Duration in the following manner: %ABondPrice z-D* x Ayield Macaulay Duration D Modified Duration D* = MktRate 1 + C/Y Use the following template to fill in and calculate the following data: D = %ABondPrice = -D* * Ayield = fill in numbers by showing work %ABondPrice -19.6901% MktRate = C/Y = D* = Ayield = [ +1% b) The "second order approximation" of %ABondPrice is to incorporate the bond's Convexity measurement: Convexity Adjustment = Convexity x (Ayield)2 %ABondPrice 2 -D* x Ayield + Convexity Adjustment new BondPrice at (YO + Ayield) Original BondPrice at Yo x (1 + %ABondPrice) Use the following template to calculate and fill in the following data: [iv] prev question's Convexity = Ayield Convexity Adjustment = Convexity * (Ayield)? = fill in numbers by showing work Convexity Adjustment = 2.5353% [v] %ABondPrice = -D* * Ayield + Convexity Adjustment = fill in numbers by showing work %ABondPrice -17.1548% [vi] c c) fill in ... From previous question's VO, current bond price @ MktRate 3% = Acutal (accurate) bond price when MktRate changes to 4% = ([viii] - [vii) = [vii] = Actual (accurate %ABondPrice = calculate [vii] [viii] [ix] calculate ... [iv] Summary data of bond, copy over from previous calculations: [vii] Macaulay-only VO Ayield D* approximation fill in with [vii] fill in with [ii] fill in with [i] fill in with [iii] Convexity [v] Convexity Adjustment fill in with [v] fill in with [iv] [vii] versus accurate Comparing the error in approximation, calculate and fill in the following: [x] [xi] = [vii] * (1 + [x]) %ABondPrice BondPrice Using Macaulay-only approximation, [ii] fill in with [ii] calculate ... Using Macaulay Duration & Convexity, [vi] fill in with [vi] calculate ... [xii] = ([xi] - [viii]) = [viii] error in approx -2.7956% (actual) price fill in with [viii] 0.2731% 27. Continuing from previous question, use Modified Duration and Convexity to approximate the percentage change in price of the bond when its market rate change from 3% to 4%. PS: to save time, calculated for you, use a Macaulay Duration D of 19.9855. a) The "first order approximation" of %ABondPrice is a linear approximation. It uses Modified Duration in the following manner: %ABondPrice z-D* x Ayield Macaulay Duration D Modified Duration D* = MktRate 1 + C/Y Use the following template to fill in and calculate the following data: D = %ABondPrice = -D* * Ayield = fill in numbers by showing work %ABondPrice -19.6901% MktRate = C/Y = D* = Ayield = [ +1% b) The "second order approximation" of %ABondPrice is to incorporate the bond's Convexity measurement: Convexity Adjustment = Convexity x (Ayield)2 %ABondPrice 2 -D* x Ayield + Convexity Adjustment new BondPrice at (YO + Ayield) Original BondPrice at Yo x (1 + %ABondPrice) Use the following template to calculate and fill in the following data: [iv] prev question's Convexity = Ayield Convexity Adjustment = Convexity * (Ayield)? = fill in numbers by showing work Convexity Adjustment = 2.5353% [v] %ABondPrice = -D* * Ayield + Convexity Adjustment = fill in numbers by showing work %ABondPrice -17.1548% [vi] c c) fill in ... From previous question's VO, current bond price @ MktRate 3% = Acutal (accurate) bond price when MktRate changes to 4% = ([viii] - [vii) = [vii] = Actual (accurate %ABondPrice = calculate [vii] [viii] [ix] calculate ... [iv] Summary data of bond, copy over from previous calculations: [vii] Macaulay-only VO Ayield D* approximation fill in with [vii] fill in with [ii] fill in with [i] fill in with [iii] Convexity [v] Convexity Adjustment fill in with [v] fill in with [iv] [vii] versus accurate Comparing the error in approximation, calculate and fill in the following: [x] [xi] = [vii] * (1 + [x]) %ABondPrice BondPrice Using Macaulay-only approximation, [ii] fill in with [ii] calculate ... Using Macaulay Duration & Convexity, [vi] fill in with [vi] calculate ... [xii] = ([xi] - [viii]) = [viii] error in approx -2.7956% (actual) price fill in with [viii] 0.2731%








