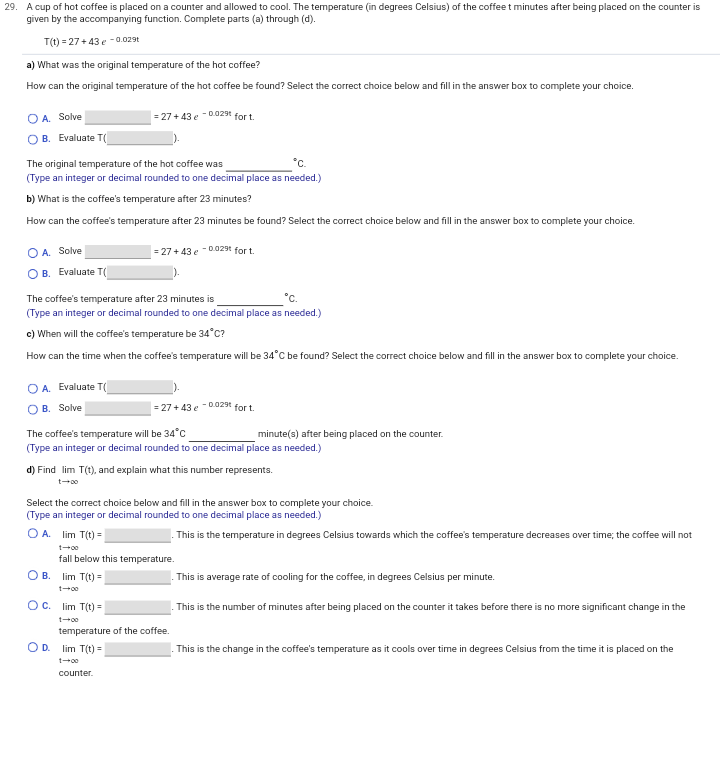
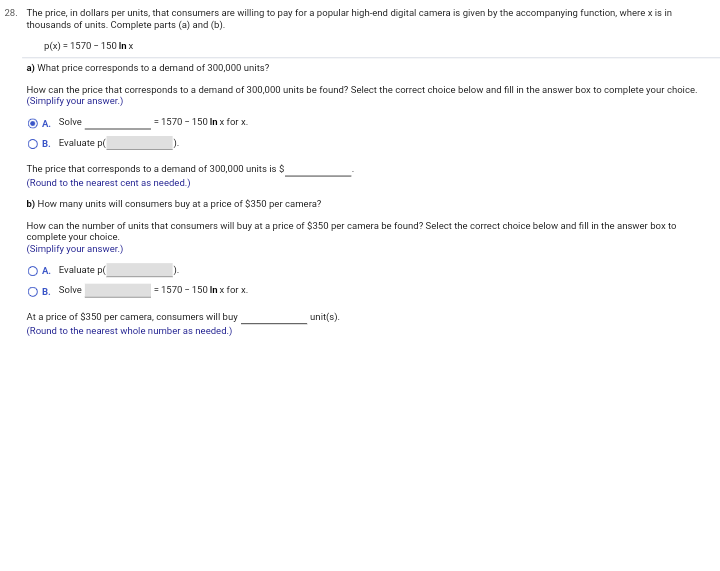
29. A cup of hot coffee is placed on a counter and allowed to cool. The temperature (in degrees Celsius) of the coffee t minutes after being placed on the counter is given by the accompanying function. Complete parts (a) through (d). T(t) = 27 +43 e - 0.029t a) What was the original temperature of the hot coffee? How can the original temperature of the hot coffee be found? Select the correct choice below and fill in the answer box to complete your choice. A. Solve =27 + 43 e - D.029% for t. O B. Evaluate T( The original temperature of the hot coffee was *C. (Type an integer or decimal rounded to one decimal place as needed.) b) What is the coffee's temperature after 23 minutes? How can the coffee's temperature after 23 minutes be found? Select the correct choice below and fill in the answer box to complete your choice. O A. Solve =27 +43 e - 0.029% for t. O B. Evaluate T( The coffee's temperature after 23 minutes is "C. Type an integer or decimal rounded to one decimal place as needed.) c) When will the coffee's temperature be 34"C? How can the time when the coffee's temperature will be 34"C be found? Select the correct choice below and fill in the answer box to complete your choice. O A. Evaluate T( O B. Solve =27 + 43 e - 0.0291 for t. The coffee's temperature will be 34"C minute(s) after being placed on the counter. (Type an integer or decimal rounded to one decimal place as needed.) d) Find lim T(1), and explain what this number represents. t-+00 Select the correct choice below and fill in the answer box to complete your choice. (Type an integer or decimal rounded to one decimal place as needed.] O A. lim T(t) = This is the temperature in degrees Celsius towards which the coffee's temperature decreases over time; the coffee will not 1-+00 fall below this temperature. O B. lim T(t) = This is average rate of cooling for the coffee, in degrees Celsius per minute. D C. lim T(t) = This is the number of minutes after being placed on the counter it takes before there is no more significant change in the -+0 temperature of the coffee. O D. lim T(t) = This is the change in the coffee's temperature as it cools over time in degrees Celsius from the time it is placed on the 1-+00 counter.7. dy Find dx 0.3 y= X dy dx 8. Differentiate the function. y= (4x# - x+3) (-x5 +5) Y'= 9. Use the Chain Rule to differentiate the following function. f(x) = 2x3 + (5x - 6)2) 7 f' (x) =5. Use the graph of y=e * and transformations to sketch the exponential function f(x) = ex - 6. Determine the domain and range. Also, determine the y-intercept, and find the equation of the horizontal asymptote. Use the graphing tool to graph the function. What is the domain of f(x) = ex - 6? "Type your answer in interval notation.) -10 10 What is the range of f(x) = ex - 6? Type your answer in interval notation.) What is the y-intercept of f(x) = ex - 6? Type an integer or a simplified fraction.) What is the horizontal asymptote of f(x) = g * - 6? "Type an equation.) 6. Use the graph of yse * and transformations to sketch the exponential function f(x) = e -* - 4. Determine the domain and range. Also, determine the y-intercept, and find the equation of the horizontal asymptote. Use the graphing tool to graph the function. What is the domain of f(x) = e - x - 4? (Type your answer in interval notation.) What is the range of f(x) = e - x - 4? 10 10 Type your answer in interval notation.) What is the y-intercept of f(x) = e - x - 4? (Type an integer or a simplified fraction.) What is the horizontal asymptote of f(x) = g - x - 4? Type an equation.)28. The price, in dollars per units, that consumers are willing to pay for a popular high-end digital camera is given by the accompanying function, where x is in thousands of units. Complete parts (a) and (b). p(x) = 1570 - 150 Inx a) What price corresponds to a demand of 300,000 units? How can the price that corresponds to a demand of 300,000 units be found? Select the correct choice below and fill in the answer box to complete your choice. (Simplify your answer.) O A. Solve = 1570 - 150 In x for x_ O B. Evaluate p The price that corresponds to a demand of 300,000 units is $ (Round to the nearest cent as needed.) b) How many units will consumers buy at a price of $350 per camera? How can the number of units that consumers will buy at a price of $350 per camera be found? Select the correct choice below and fill in the answer box to complete your choice. (Simplify your answer.) O A. Evaluate p( O B. Solve = 1570 - 150 In x for x. At a price of $350 per camera, consumers will buy unit(s). (Round to the nearest whole number as needed.)