Question: 3. (3 points) Let $y_{1}, ldots, y_{n}$ be numbers, and $bar(y)=frac{1}{n} sum_{i=1}^{n} y_{i}$. Show that $sum_{i=1}^{n}left(y_{i}-bar{y} ight)^{2}=sum_{i=1}^{n} y_{i}^{2}-n bar{y}^{2} .$ SP.PB. 189

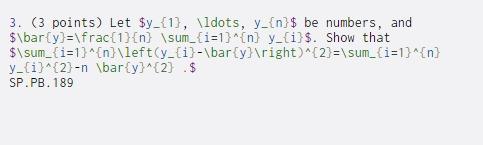
$3. (3 points) Let $y_{1}, \ldots, y_{n}$ be numbers, and $\bar(y)=\frac{1}{n}$

3. (3 points) Let $y_{1}, \ldots, y_{n}$ be numbers, and $\bar(y)=\frac{1}{n} \sum_{i=1}^{n} y_{i}$. Show that $\sum_{i=1}^{n}\left(y_{i}-\bar{y} ight)^{2}=\sum_{i=1}^{n} y_{i}^{2}-n \bar{y}^{2} .$ SP.PB. 189

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

4 (a) (10 points) Can et - 1 be the solution of the differential equation of the form y"+ p(t )y' + q(t)y= 0,where p(t) and q(t) are continuous over an open interval containing 0? Justify your answer...

A comparative study is performed; you are given the following information. ? The total number of subjects equals 29. ? The observed value of the test statistic is greater than 0. I used the website...

4. (a) (10 points) Let y1, y2 be a fundamental pair of solutions of the differential equation 3 x?y" + 3xy' + (2 + )y=0. Determine the Wronskian W(y1, y2) upto a constant. (b) (12 points) Given that...

3. (6 points) Let X1, X2, ..., Xs be a random sample of SAT mathematics scores, assumed to be N(ux, 02), and let Y1, Y2, ..., Ys be and independent random sample of SAT verval scores, assumed to be...

Show that the sample means for the two sets are close. Specically, show: are) are) 5 2 (2) This is referred to aspn having sensitivity nil. (b) (1 point) For any xedS, explain why pg,\" (5) is...

4. (25 POINTS) Let Y1, ..., Yn be iid with N(Mo, 62) distribution, where Mo is treated as a known value. Consider the statistic n 62 = - ( Y1 - MO ) 2 n i= 1 Show that 62 is a consistent estimator of...

( 3 0 points ) Let Y 1 and Y 2 denote two continuous random variables. The joint pdf of Y 1 and Y 2 is given by Y 1 Y 2 c V ( Y 1 Y 2 ) C o v ( Y 1 Y 2 , Y 2 ) ( 2 Y 1 Y 2 , Y 2 ) 2 Y 1 Y 2 Y 2

please answer part 1,2 Consider the following game, where player 1 chooses a strategy U or M or D and player 2 chooses a strategy L or R. 1. (2 points) Under what conditions on the parameters is U a...

3. [7 marks] Let y1, ..., In be a set of responses and let $1, ..., 'n be a corresponding set of predictors lying in the interval [a, b]. Recall that a cubic smoothing spline is the function obtained...

Problem 3. (20 points) Let X = (X1, X2, ...Xn) be a sequence of n integers and Y = (y1, Y2, ...Ym) is a subsequence of X if Y can be obtained from X by delet- ing zero or more elements from X. Y is a...

Consider the PD control system shown in Figure 10.7.1. Suppose that I = 20 and c = 10. The specifications require the steady-state error due to a unit-step command to be zero and the steady-state...

While auditing XYZ Ltd your audit senior found that senior accounts payable clerk, Jillian Perkins, had been creating fake creditor's invoices from non-operating companies that she owned, for goods...

The company secretary of Beech Ltd has in the past been permitted to order office equipment and stationery for the company but no single transaction has exceeded 500. Recently, without the knowledge...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

2. The Interactive Patient is a realistic interactive computer simulation of a patients visit to a physicians office. The Interactive Patient is a Web-based training program used to train medical...

7. What are some potential problems with using virtual reality technology for training?

6. Is all Internet training the same? Explain.