3. Answer the following questions by using the sensitivity analysis results (that is, the ranging results) from Question 2. Do NOT solve the problem again by using any computer software.

(a) If the profit from a unit of model A+ increases from $100 to $110, will the optimal number of units of the three models manufactured change? Will the total profit change? What will be the new optimal number of units of the three models and the new profit?

(b) The company has an opportunity to obtain some extra manufacturing time. What is the maximum price the company should pay for each additional hour of manufacturing time, and how many hours of manufacturing time should they obtain at that price?

(c) The company has an opportunity to buy some extra fans. What is the maximum price the company should pay for each additional fan, and how many fans should they buy at that price?

Here is the original problem with the answers:

HERE IS QUESTION 1:

An air conditioning company manufactures three home air conditioners: model A, model A+ and model A++. The profits per unit are $70, $100, and $145, respectively. The production requirements per unit and the availability of the three resources are given below:

	Model A	Model A+	Model A++	Available
Number of fans	1	1	1	400
Number of cooling coils	2	2	4	600
Manufacturing Time	12	16	20	4500 hours

How many model A, model A+ and model A++ air conditioners should the company manufacture in order to maximize profit?

Formulate a linear programming model for the above situation by determining

(a) The decision variables.

(b) Determine the objective function. What does it represent?

(c) Determine all the constraints. Briefly describe what each constraint represents.

HERE ARE THE RESULTS:

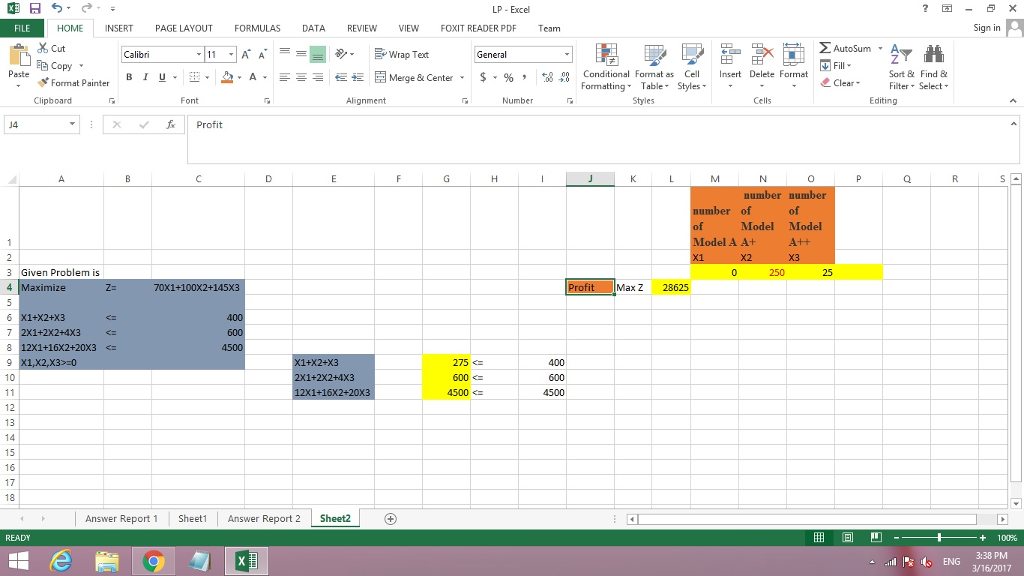
Let the number of Model A be x1

Let the number of Model A+ be x2

Let the number of Model A++ be x3

Constraints

x1 + x2 + x3

2x1 + 2x2 + 4x2

12x1 + 16x2 + 20x3

Objective Function:

Profit Z = 70x1 + 100x2 + 145x3

(a) The decision variables are the suitable values of x1,x2 and x3 for which all the constriants are met and the profit function function Z is maximized

(b) The objective function Z = 70x1 + 100x2 + 145x3 represents the amount of profit that will be going to generate after selling x1 units of A, x2 units of A+ and x3 units of A++

(c) The constraints are given below

x1 + x2 + x3

2x1 + 2x2 + 4x2

12x1 + 16x2 + 20x3

Question 2)

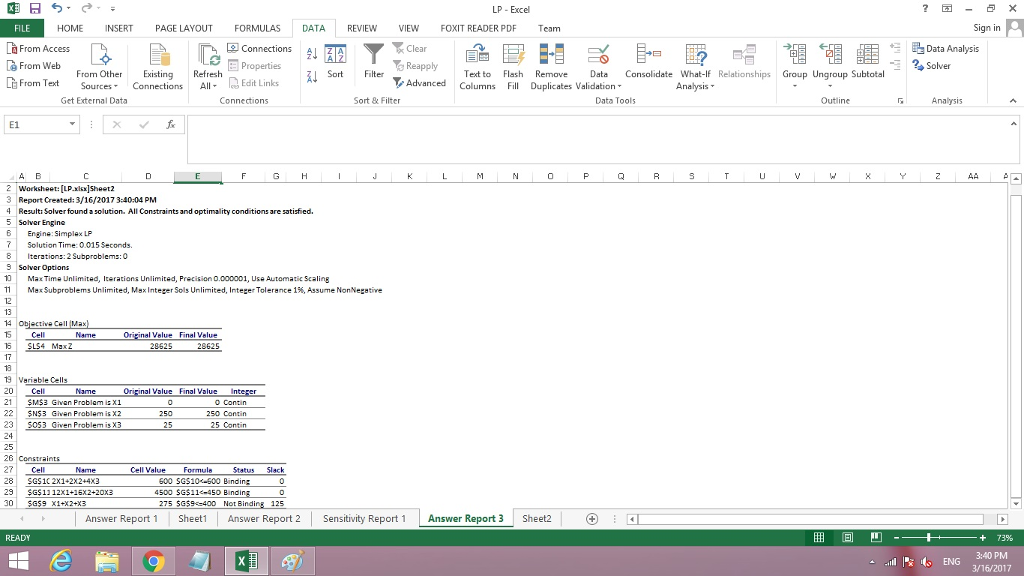
Find the computer solution, including the ranging (sensitivity analysis) results, for Question 1 by using QM for Windows or Excel. Determine the optimal solution (including the decision variables and the slack/surplus variables) and optimal profit. Interpret the optimal solution and optimal profit:

Answer:

LP Excel HOME NSERT PAGE LAYOUT FORMULAS DATA REVIEW VIEW FOXIT READER PDF Team cut AutoSum EE Copy Calibri A A E Wrap Text General EE BE Format Painter B I u a. A EE E Merge & Center %8.08 Condit Format as Cel rt Delete Format Formatting Table Styl Sort & Find & 2Clear lter Select Clipboard Font Alignment Number Editing Profit number of Model Model Model A At 3 Given Problem is Profit Max z 28625 Maximize 70X1 100X2-145X3 1+X2+X3 2X1+16X2+20X3 X3> 0 1+X2+X3. 275 +2X2+MX3 600 1+16X2+20X Answer Report 1 Sheet Answer Report 2 Sheet2 El READY x Sign in 3:38 PM 3/16/2017