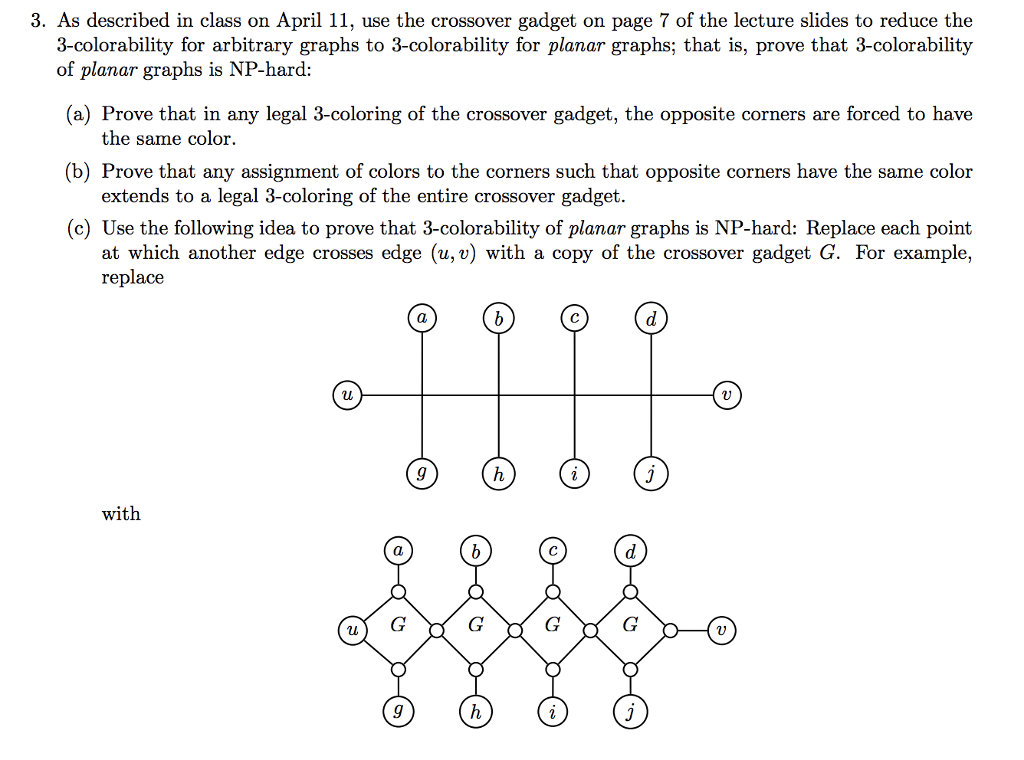
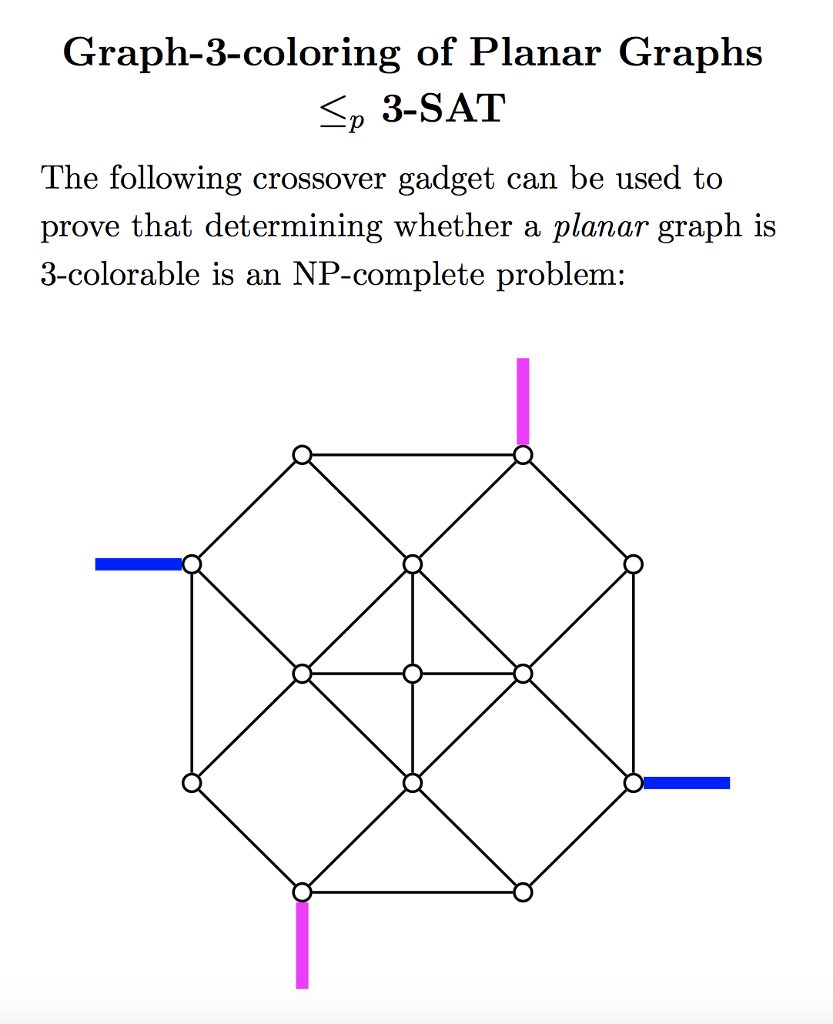
3. As described in class on April 11, use the crossover gadget on page 7 of the lecture slides to reduce the 3-colorability for arbitrary graphs to 3-colorability for planar graphs; that is, prove that 3-colorability (a) Prove that in any legal 3-coloring of the crossover gadget, the opposite corners are forced to have (b) Prove that any assignment of colors to the corners such that opposite corners have the same color (c) Use the following idea to prove that 3-colorability of planar graphs is NP-hard: Replace each point of planar graphs is NP-hard: the same color extends to a legal 3-coloring of the entire crossover gadget at which another edge crosses edge (u, v) with a copy of the crossover gadget G. For example, replace with 0 3. As described in class on April 11, use the crossover gadget on page 7 of the lecture slides to reduce the 3-colorability for arbitrary graphs to 3-colorability for planar graphs; that is, prove that 3-colorability (a) Prove that in any legal 3-coloring of the crossover gadget, the opposite corners are forced to have (b) Prove that any assignment of colors to the corners such that opposite corners have the same color (c) Use the following idea to prove that 3-colorability of planar graphs is NP-hard: Replace each point of planar graphs is NP-hard: the same color extends to a legal 3-coloring of the entire crossover gadget at which another edge crosses edge (u, v) with a copy of the crossover gadget G. For example, replace with 0