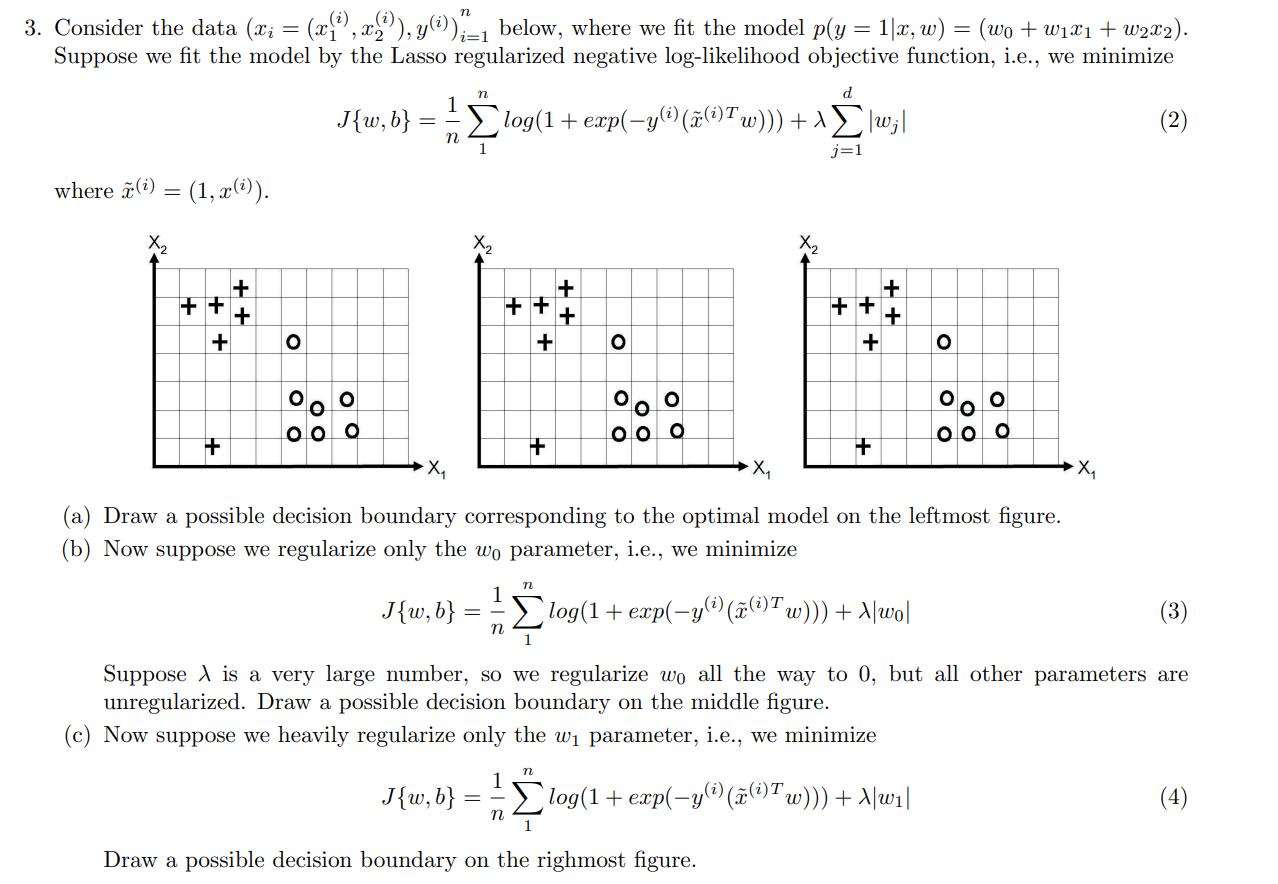
3. Consider the data (x; = (x(), , y());=1 below, where we fit the model p(y = 1|x, w) = (wo + 1x1 + W2x2). Suppose we fit the model by the Lasso regularized negative log-likelihood objective function, i.e., we minimize where (i) = (1, x(i)). 1 n d J{w,b} === log(1 + exp(y) (x(Tw)}}+\[\wz n j=1 X2 + ++ + + 00 + X2 + ++ + + + X2 ++ ++ + + + 00 (a) Draw a possible decision boundary corresponding to the optimal model on the leftmost figure. (b) Now suppose we regularize only the wo parameter, i.e., we minimize J{w,b} n == log(1+ exp(-y() ( (i) Tw))) + A|wo| n Suppose is a very large number, so we regularize wo all the way to 0, but all other parameters are unregularized. Draw a possible decision boundary on the middle figure. (c) Now suppose we heavily regularize only the w parameter, i.e., we minimize J{w, b} = n 1 n log(1+ exp(y (i) ((i)Tw))) + A|w1| 1 Draw a possible decision boundary on the righmost figure. (4)