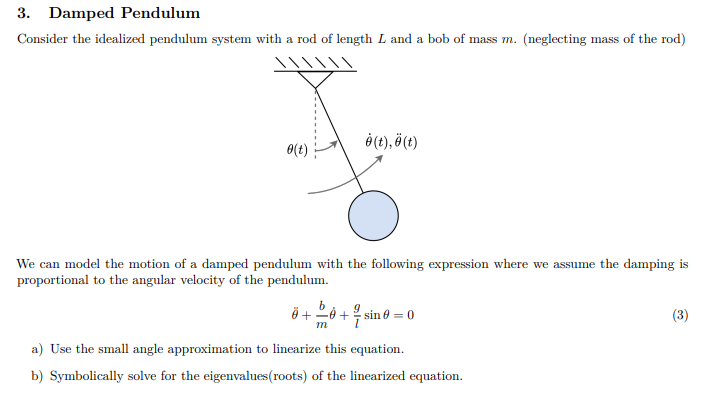
3. Damped Pendulum Consider the idealized pendulum system with a rod of length L and a bob of mass m. (neglecting mass of the rod) 0(t) (t), (t) We can model the motion of a damped pendulum with the following expression where we assume the damping is proportional to the angular velocity of the pendulum. b 0+0+ sin 0 = 0 m a) Use the small angle approximation to linearize this equation. b) Symbolically solve for the eigenvalues (roots) of the linearized equation. (3) c) Find the symbolic Jacobian of the original(non-linear) expression. For the following parts, let m = 1 kg, L = 1m, and g = 9.81 m/s. Solve all parts for b=0Ns/m and b=0.5 Ns/m. d) Use the Jacobian to find the local eigenvalues for the two equilibrium points, (0,0) = (0,0) and (0,0) = (,0). e) Plot the local solution for the equilibrium point (0,0) = (0,0) using the initial data 0(0) = 0.5 and (0) = 0. Comment on what you see. f) Plot the solution from the small angle approximation and the local solution derived from the equilibria (0,0) = (0,0), using the initial data 0(0) = 0.5 and (0) = 0. Comment on what you see. g) Use ode 45 to solve the original nonlinear expression for the same initial conditions. Plot this with the results from the small angle approximation. Comment on what you see.