
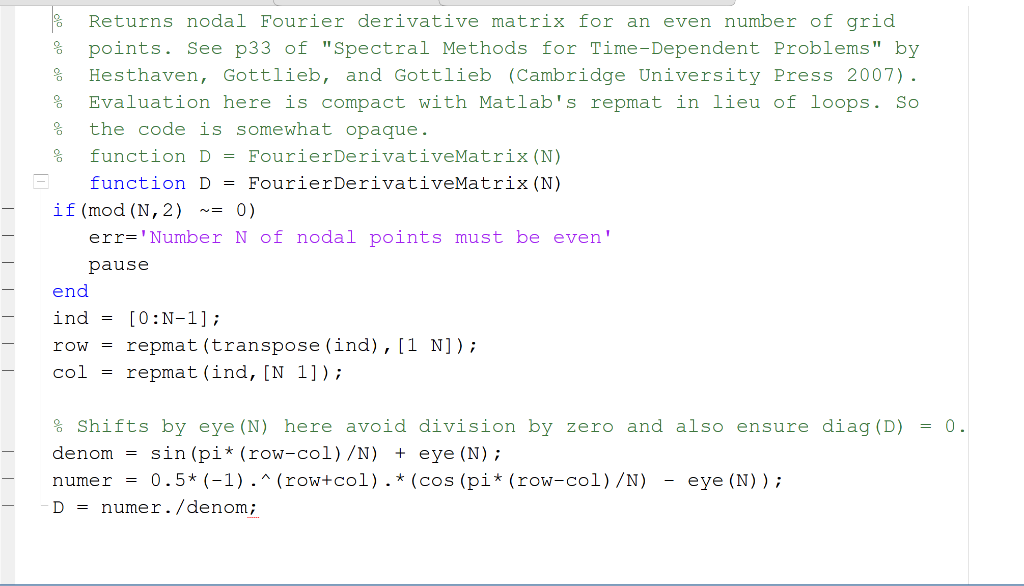
3. Here we approximate f'(x) for the periodic function f(x) defined on (0,27] using a nodal Fourier method (please don't worry if you have never heard of such). Define a grid of x values via Ck = 2T (k 1)/N, for k = 1,2,...,N, and here assume throughout that N is an even integer. Define a column vector f with components fx = f(Ik), and a derivative matrix D ERNXN with entries 1(-1);+k-2 cot(T(j k)/N) if j #k 0 if j =k djk = { }{-1}+. The components of g = Df are then approximations of the values f'(xk) for k = 1, 2, ... ,N. A MATLAB function FourierDerivativeMatrix which returns D is available on UNM Learn. For f(x) = exp(sin x) use this function to approximate f'(T) as the component g(1 + N/2) = 91+N/2. That is approximate f'(T) as the (1+N/2)st component of Df. For N = 4,8, 12, 16, 20, 24, 28, 32, 36 compute the error (in absolute value) between the approximation and the exact answer (still 1). Plot the set of errors versus N. What do you observe? Returns nodal Fourier derivative matrix for an even number of grid g points. See p33 of "Spectral Methods for Time-Dependent Problems" by g Hesthaven, Gottlieb, and Gottlieb (Cambridge University Press 2007). Evaluation here is compact with Matlab's repmat in lieu of loops. So the code is somewhat opaque. function D = Fourier DerivativeMatrix (N) function D = Fourier DerivativeMatrix (N) if (mod (N, 2) ~= 0 err='Number N of nodal points must be even' pause end ind [0:N-1]; row repmat (transpose (ind), [1 N]); col = repmat (ind, [N 1]); % Shifts by eye (N) here avoid division by zero and also ensure diag (D) = 0. denom = sin(pi* (row-col) /N) + eye (N); 0.5* (-1). ^ (row+col).* (cos (pi* (row-col) /N) - eye (N)); D = numer./denom; numer 3. Here we approximate f'(x) for the periodic function f(x) defined on (0,27] using a nodal Fourier method (please don't worry if you have never heard of such). Define a grid of x values via Ck = 2T (k 1)/N, for k = 1,2,...,N, and here assume throughout that N is an even integer. Define a column vector f with components fx = f(Ik), and a derivative matrix D ERNXN with entries 1(-1);+k-2 cot(T(j k)/N) if j #k 0 if j =k djk = { }{-1}+. The components of g = Df are then approximations of the values f'(xk) for k = 1, 2, ... ,N. A MATLAB function FourierDerivativeMatrix which returns D is available on UNM Learn. For f(x) = exp(sin x) use this function to approximate f'(T) as the component g(1 + N/2) = 91+N/2. That is approximate f'(T) as the (1+N/2)st component of Df. For N = 4,8, 12, 16, 20, 24, 28, 32, 36 compute the error (in absolute value) between the approximation and the exact answer (still 1). Plot the set of errors versus N. What do you observe? Returns nodal Fourier derivative matrix for an even number of grid g points. See p33 of "Spectral Methods for Time-Dependent Problems" by g Hesthaven, Gottlieb, and Gottlieb (Cambridge University Press 2007). Evaluation here is compact with Matlab's repmat in lieu of loops. So the code is somewhat opaque. function D = Fourier DerivativeMatrix (N) function D = Fourier DerivativeMatrix (N) if (mod (N, 2) ~= 0 err='Number N of nodal points must be even' pause end ind [0:N-1]; row repmat (transpose (ind), [1 N]); col = repmat (ind, [N 1]); % Shifts by eye (N) here avoid division by zero and also ensure diag (D) = 0. denom = sin(pi* (row-col) /N) + eye (N); 0.5* (-1). ^ (row+col).* (cos (pi* (row-col) /N) - eye (N)); D = numer./denom; numer








