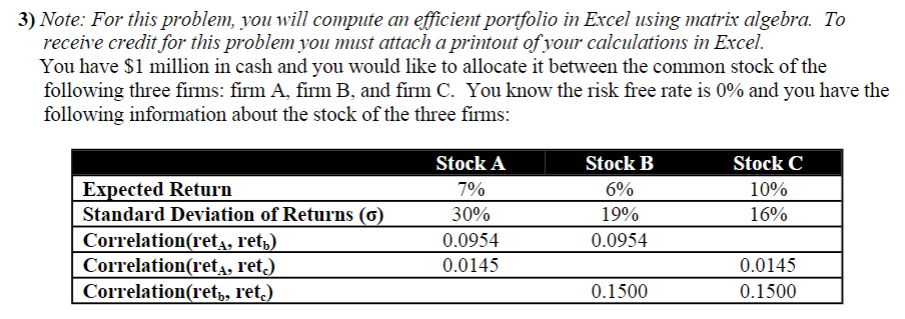

3) Note: For this problem, you will compute an efficient portfolio in Excel using matrix algebra. To receive credit for this problem you must attach a printout of your calculations in Excel. You have $1 million in cash and you would like to allocate it between the common stock of the following three firms: firm A, firm B, and firm C. You know the risk free rate is 0% and you have the following information about the stock of the three firms: Stock A 7% 30% 0.0954 0.0145 Expected Return Standard Deviation of Returns (6) Correlation(reta, ret) Correlation(reta, ret.) Correlationret, ret.) Stock B 6% 19% 0.0954 Stock C 10% 16% 0.0145 0.1500 0.1500 d) Type the matrix A, and the vector bo into Excel and compute the inverse of matrix A, using the function =MINVERSE. Note: To use matrix functions in Excel, you need to highlight an area that has the same dimensions as the matrix that will result from the calculation. For example, if matrix A, is in cells A6 to E10 and you'd like to create the answer in cells A29 to E33, you would highlight cells A29 to E33, type=MINVERSE(A6:AE10) and hit ctr + shift + enter at the same time to calculate the result. e) Using your answer from part (d), calculate the optimal weight vector using the matrix multiplication function MMULT. You want to multiply the inverse of A, and vector bo. Again, you need to highlight an area that has the same dimension as the vector that will result from the calculation. For example, if you'd like the optimal weight vector to appear in cells A41 to A45, highlight A41 to A45 and type=MMULT(A29:E33,A18:A22), where A29 to E33 is the location of Az and A18 to A22 is the location of bo. What is the optimal weight vector? f) Given your answer in (e), what is the matrix algebra equation for the expected return on the optimal portfolio? What is the expected return on the optimal portfolio? [Hint: Use the MMULT function again and multiply the transpose of the optimal weight vector by the expected return vector a.] g) Given your answer in (C), what is the matrix algebra equation for the expected standard deviation on the optimal portfolio? What is the expected standard deviation on the optimal portfolio? [Hint: you will use the MMULT function again, but you need to break the problem into two steps. First, multiply the transpose of the optimal weights by the covariance matrix; the answer will be a 1x3 vector. Then, multiply this vector by the optimal weight vector to receive the expected portfolio standard deviation.] 3) Note: For this problem, you will compute an efficient portfolio in Excel using matrix algebra. To receive credit for this problem you must attach a printout of your calculations in Excel. You have $1 million in cash and you would like to allocate it between the common stock of the following three firms: firm A, firm B, and firm C. You know the risk free rate is 0% and you have the following information about the stock of the three firms: Stock A 7% 30% 0.0954 0.0145 Expected Return Standard Deviation of Returns (6) Correlation(reta, ret) Correlation(reta, ret.) Correlationret, ret.) Stock B 6% 19% 0.0954 Stock C 10% 16% 0.0145 0.1500 0.1500 d) Type the matrix A, and the vector bo into Excel and compute the inverse of matrix A, using the function =MINVERSE. Note: To use matrix functions in Excel, you need to highlight an area that has the same dimensions as the matrix that will result from the calculation. For example, if matrix A, is in cells A6 to E10 and you'd like to create the answer in cells A29 to E33, you would highlight cells A29 to E33, type=MINVERSE(A6:AE10) and hit ctr + shift + enter at the same time to calculate the result. e) Using your answer from part (d), calculate the optimal weight vector using the matrix multiplication function MMULT. You want to multiply the inverse of A, and vector bo. Again, you need to highlight an area that has the same dimension as the vector that will result from the calculation. For example, if you'd like the optimal weight vector to appear in cells A41 to A45, highlight A41 to A45 and type=MMULT(A29:E33,A18:A22), where A29 to E33 is the location of Az and A18 to A22 is the location of bo. What is the optimal weight vector? f) Given your answer in (e), what is the matrix algebra equation for the expected return on the optimal portfolio? What is the expected return on the optimal portfolio? [Hint: Use the MMULT function again and multiply the transpose of the optimal weight vector by the expected return vector a.] g) Given your answer in (C), what is the matrix algebra equation for the expected standard deviation on the optimal portfolio? What is the expected standard deviation on the optimal portfolio? [Hint: you will use the MMULT function again, but you need to break the problem into two steps. First, multiply the transpose of the optimal weights by the covariance matrix; the answer will be a 1x3 vector. Then, multiply this vector by the optimal weight vector to receive the expected portfolio standard deviation.]








