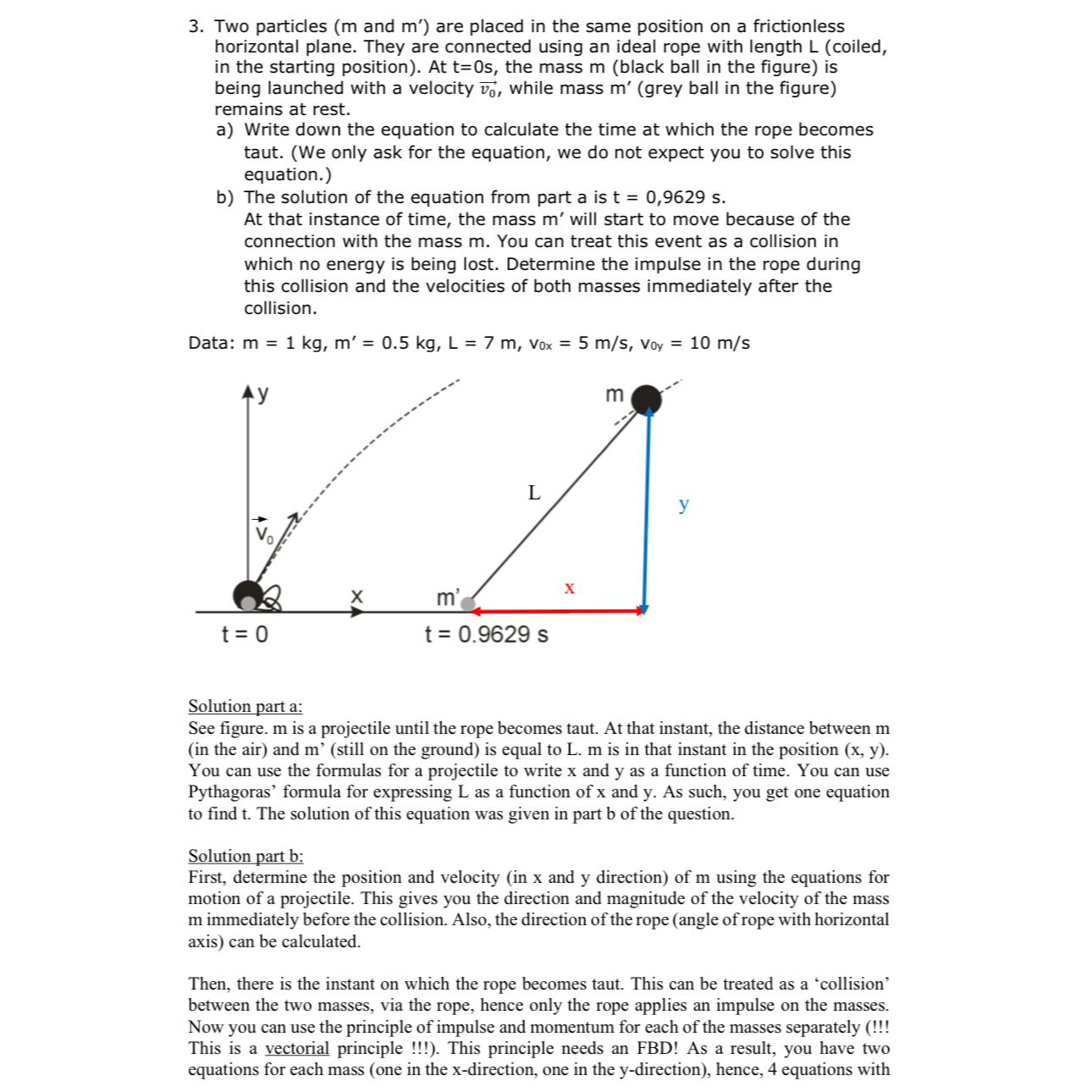
3. Two particles (m and m) are placed in the same position on a frictionless horizontal plane. They are connected using an ideal rope with length L (coiled, in the starting position). At t=0s, the mass m (black ball in the figure) is being launched with a velocity, while mass m' (grey ball in the figure) remains at rest. a) Write down the equation to calculate the time at which the rope becomes taut. (We only ask for the equation, we do not expect you to solve this equation.) b) The solution of the equation from part a is t = 0,9629 s. At that instance of time, the mass m' will start to move because of the connection with the mass m. You can treat this event as a collision in which no energy is being lost. Determine the impulse in the rope during this collision and the velocities of both masses immediately after the collision. Data: m = 1 kg, m' = 0.5 kg, L = 7 m, Vox = 5 m/s, Voy = 10 m/s t = 0 L m' t = 0.9629 s X m y Solution part a: See figure. m is a projectile until the rope becomes taut. At that instant, the distance between m (in the air) and m' (still on the ground) is equal to L. m is in that instant in the position (x, y). You can use the formulas for a projectile to write x and y as a function of time. You can use Pythagoras' formula for expressing L as a function of x and y. As such, you get one equation to find t. The solution of this equation was given in part b of the question. Solution part b: First, determine the position and velocity (in x and y direction) of m using the equations for motion of a projectile. This gives you the direction and magnitude of the velocity of the mass mimmediately before the collision. Also, the direction of the rope (angle of rope with horizontal axis) can be calculated. Then, there is the instant on which the rope becomes taut. This can be treated as a 'collision' between the two masses, via the rope, hence only the rope applies an impulse on the masses. Now you can use the principle of impulse and momentum for each of the masses separately (!!! This is a vectorial principle !!!). This principle needs an FBD! As a result, you have two equations for each mass (one in the x-direction, one in the y-direction), hence, 4 equations with