Answered step by step

Verified Expert Solution

Link Copied!

Question

1 Approved Answer

Posted on Jan 03, 2023

3.10 Show that a norm ||-|| on a linear space X is generated by a scalar product if and only if the parallelogram equality

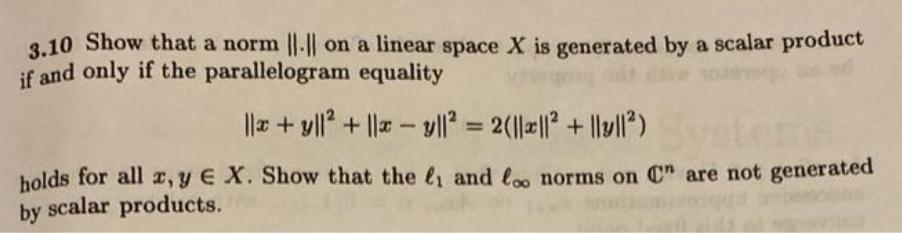
3.10 Show that a norm ||-|| on a linear space X is generated by a scalar product if and only if the parallelogram equality ||x+y||+ ||xy|| = 2(||*|| + ||y||) holds for all x, y EX. Show that the and loo norms on C" are not generated by scalar products.

Step by Step Solution

★★★★★

3.29 Rating (146 Votes )

There are 3 Steps involved in it

Step: 1

A norm on a linear space X is generated by a scalar product if and only if the parallelogram ... blur-text-image

Get Instant Access to Expert-Tailored Solutions

See step-by-step solutions with expert insights and AI powered tools for academic success

Step: 2

Step: 3

Ace Your Homework with AI

Get the answers you need in no time with our AI-driven, step-by-step assistance

Get Started

Recommended Textbook for

Linear Algebra with Applications

Authors: Steven J. Leon

7th edition

131857851, 978-0131857858

More Books

Students also viewed these Accounting questions

Question

★★★★★

The temperature is not 90 if and only if the air conditioner is not working, or the apartment is not hot. Write the statements in symbolic form. Let p: The temperature is 90. q: The air conditioner...

Answered: 1 week ago

Question

★★★★★

Show that a complex sequence is bounded if and only if the two corresponding sequences of the real parts and of the imaginary parts are bounded.

Answered: 1 week ago

Question

★★★★★

Show that A -1 exists if and only if the eigenvalues 1 , , n are all nonzero, and then A -1 has the eigenvalues 1/ 1 , ,1/ n .

Answered: 1 week ago

Question

★★★★★

A square duct, 30 cm by 30 cm, is maintained at a constant temperature of 30oC and an airstream of 50oC and 1 atm is forced across it with a velocity of 6 m/s. Calculate the heat gained by the duct....

Answered: 1 week ago

Question

★★★★★

Briefly contrast the accounting procedures in perpetual and periodic inventory systems.

Answered: 1 week ago

Question

★★★★★

Fitness Pro paid $286.99 for a set of PowerBlock weights. Overhead is 23% of the regular selling price and profit is 17% of the regular selling price. During a clearance sale, the set was sold at a...

Answered: 1 week ago

Question

★★★★★

Discuss how family structure influences household investment decision-making behavior.

Answered: 1 week ago

Question

★★★★★

Red Fire Inc. produces fire trucks. The company uses a normal job-order costing system to calculate its cost of goods manufactured. The company's policy is to price its job at cost plus 30% markup....

Answered: 1 week ago

Question

★★★★★

What is the fundamental difference in a general stock redemption vs. a Liquidating Distribution? What are the income tax consequences?

Answered: 1 week ago

Question

★★★★★

Yolanda has the option of investing in two different mutual funds. The return in the random walk fund tends to fluctuate wildly, earning substantial positive returns one year only to realize negative...

Answered: 1 week ago

Question

★★★★★

please answer correctly 1. What is the decision variable 2. What is the objective function 3. List the constraints Daycare Problem Joyce and Marvin run a daycare for preschoolers. They are trying to...

Answered: 1 week ago

Question

★★★★★

Exeter Division of Wetherby Labs acquired an asset with a cost of $800,000 and a four-year life. The cash flows from the asset, considering the effects of Inflation, were scheduled as follows: Year 1...

Answered: 1 week ago

Question

★★★★★

Flyaway Rural Airlines is planning to add the following three aitcraft to its fleet, an Airbus, a Boeing and an fimbraer, with the following characteristic: Part A: Calculate the weighted average...

Answered: 1 week ago

Question

★★★★★

A C D E G H 1 The finacial manager of a company is preparing the monthly budget report. He aims to understand which of expenses have been over budget in the previous year. 2 You are required to: 3...

Answered: 1 week ago

Question

★★★★★

Question 1(15 Marks): A firm produces one good with a technology given by the production function y = f (x) = x1/3. The factor price w and the price p for the good are fixed. a) Explore whether the...

Answered: 1 week ago

Question

★★★★★

A large country named H is considering an import tariff to protect the industry that produces good X. The world's excess supply curve is P=1000+3X. Country H's excess demand curve is P=8000-50X. a.)...

Answered: 1 week ago

Question

★★★★★

We are evaluating a project that costs $670,000, has a five-year life, and has no salvage value. Assume that depreciation is straight-line to zero over the life of the project. Sales are projected at...

Answered: 1 week ago

Question

★★★★★

In the operation of an automated production line with storage buffers, what does it mean if a buffer is nearly always empty or nearly always full?

Answered: 1 week ago

Question

★★★★★

Prove the Frobenius theorem in the case where A is a 2 2 matrix.

Answered: 1 week ago

Question

★★★★★

Let A be an n x n matrix and let A be an eigenvalue of A whose eigenspace has dimension k. where I where I is the k x k identity mairk. (b) Use Theorem 6.1.1 to show that is an eigenaIue of A with...

Answered: 1 week ago

Question

★★★★★

Let x1, x2, ..., xn be the roots of the Legendre polynomial Pn. If the Ai's are defined as in Exercise 15, then the quadrature formula will be exact for all polynomials of degree less than 2n. (a) If...

Answered: 1 week ago

Question

★★★★★

Require you to manipulate a formula from the inside-back cover to isolate a different variable on the left-hand side. Rearrange formula (13-1) to isolate i on the left side.

Answered: 1 week ago

Question

★★★★★

Require you to manipulate a formula from the inside-back cover to isolate a different variable on the left-hand side. Rearrange formula (4-2) to isolate d1 on the left side.

Answered: 1 week ago

Question

★★★★★

Require you to manipulate a formula from the inside-back cover to isolate a different variable on the left-hand side. Rearrange formula (4-2) to isolate d3 on the left side.

Answered: 1 week ago

Previous Question Next Question