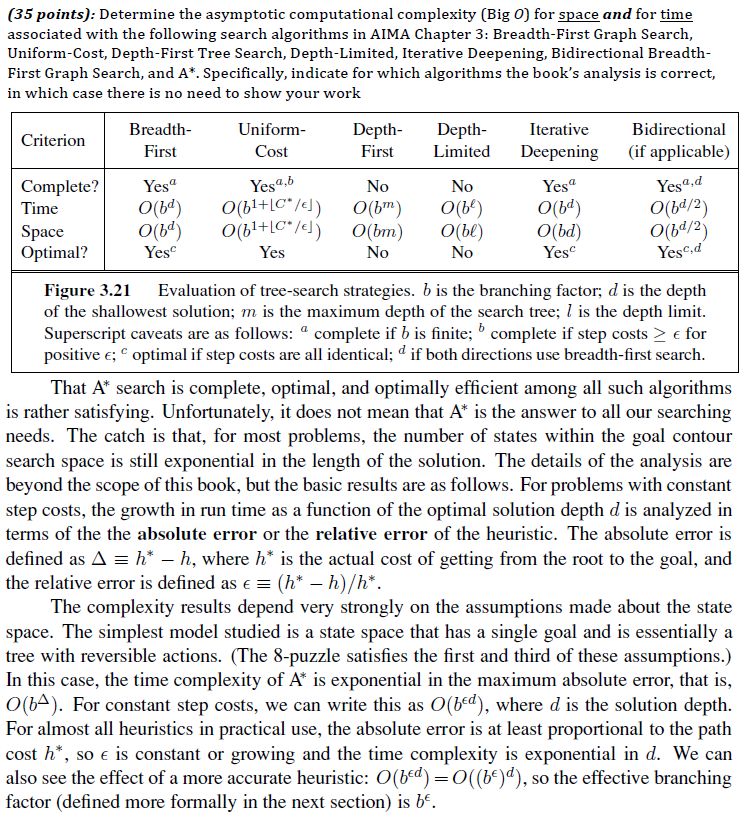
(35 points): Determine the asymptotic computational complexity (Big O) for space and for time associated with the following search algorithms in AIMA Chapter 3: Breadth-First Graph Search, Uniform-Cost, Depth-First Tree Search, Depth-Limited, Iterative Deepening, Bidirectional Breadth First Graph Search, and A*. Specifically, indicate for which algorithms the book's analysis is correct, in which case there is no need to show vour work Breadth- First Uniform- Cost Depth Bidirectional First Lited Deepening if applicable) Depth Iterative Criterion Complete? es es Yesa O(bd/2) ime Optimal? Yes Figure 3.21 Evaluation of tree-search strategies. b is the branching factor; d is the depth of the shallowest solution; m is the maximum depth of the search tree; 1 is the depth limit. Superscript caveats are as follows: a complete if b is finite; b complete if step costs 2 e for positive e; optimal if step costs are all identical; d if both directions use breadth-first search That A* search is complete, optimal, and optimally efficient among all such algorithms is rather satisfying. Unfortunately, it does not mean that A* is the answer to all our searching needs. The catch is that, for most problems, the number of states within the goal contour search space is still exponential in the length of the solution. The details of the analysis are beyond the scope of this book, but the basic results are as follows. For problems with constant step costs, the growth in run time as a function of the optimal solution depth d is analyzed in terms of the the absolute error or the relative error of the heuristic. The absolute error is defined as h*-h, where h* is the actual cost of getting from the root to the goal, and the relative error is defined as (h*-h)/h". The complexity results depend very strongly on the assumptions made about the state space. The simplest model studied is a state space that has a single goal and is essentially a tree with reversible actions. (The 8-puzzle satisfies the first and third of these assumptions.) In this case, the time complexity of A* is exponential in the maximum absolute error, that is O(bA). For constant step costs, we can write this as O(bed), where d is the solution depth For almost all heuristics in practical use, the absolute error is at least proportional to the path cost h*, so e is constant or growing and the time complexity is exponential in d. We can also see the effect of a more accurate heuristic: O(bed (bd), so the effective branching factor (defined more formally in the next section) is be