36 and 44 please

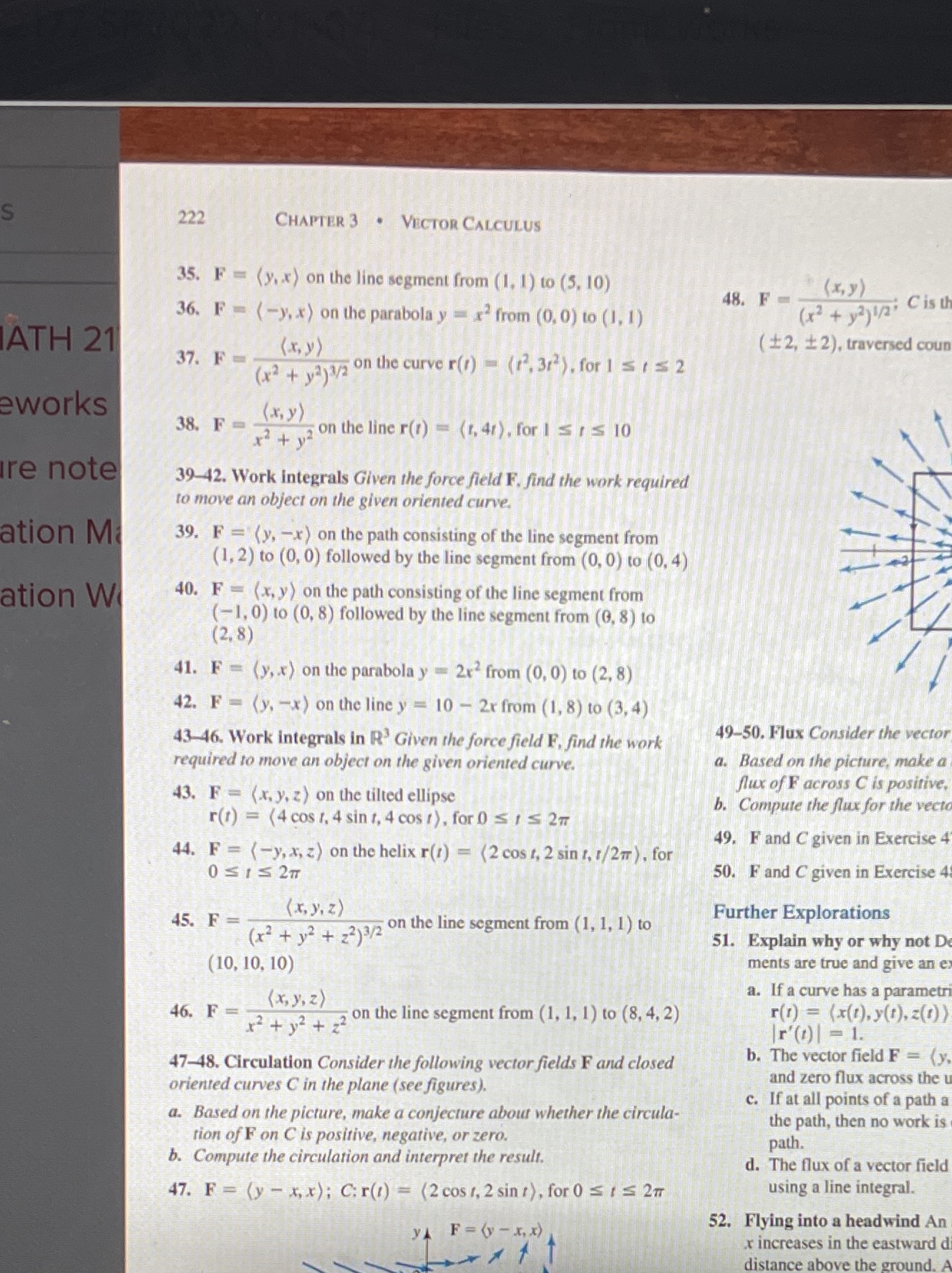
222 CHAPTER 3 . VECTOR CALCULUS 35. F = (y,x) on the line segment from (1, 1) to (5, 10) ( x,y ) 48. F - 36. F - (-y, x) on the parabola y = x2 from (0, 0) to (1, 1) (x3 + yayin; Cis u ATH 21 ( x , y ) ( $2, + 2), traversed coun 37. F- (x2 + yajara on the curve r() - (r', 31 ). for 1 5 1 5 2 eworks 38. F - ( x, y ) x2 + on the line r() = (r, 41), for I S t s 10 Ire note 39-42. Work integrals Given the force field F. find the work required to move an object on the given oriented curve. ation M 39. F = (y, -x) on the path consisting of the line segment from (1, 2) to (0, 0) followed by the line segment from (0, 0) to (0, 4) ation W 40. F = (x, y ) on the path consisting of the line segment from (-1, 0) to (0, 8) followed by the line segment from (6, 8) to (2, 8) 41. F = (y, x) on the parabola y = 2x2 from (0, 0) to (2, 8) 42. F - (y, -x) on the line y = 10 - 2x from (1, 8) to (3, 4) 43-46. Work integrals in R' Given the force field F, find the work 49-50. Flux Consider the vector required to move an object on the given oriented curve. a. Based on the picture, make a flux of F across C is positive, 43. F = (x, y, z) on the tilted ellipse b. Compute the flux for the vect r(1) = (4 cos , 4 sin t, 4 cos () . for 0 S t S 217 49. F and C given in Exercise 4 44. F = (-y, x, z) on the helix r(1) = (2 cost, 2 sin t, 1/2Tr) . for OSIS2T 50. F and C given in Exercise 4 45. F = ( x, y. z) Further Explorations (x2 + y2 + z2)3/2 on the line segment from (1, 1, 1) to 51. Explain why or why not D (10, 10, 10) ments are true and give an e a. If a curve has a parametr 46. F = (x, y, z) x2 + y2 + ,2 on the line segment from (1, 1, 1) to (8, 4, 2) r(1) = (x(1), y(t), z(1) |r'(t) = 1. 47-48. Circulation Consider the following vector fields F and closed b. The vector field F = (y oriented curves C in the plane (see figures). and zero flux across the u c. If at all points of a path a a. Based on the picture, make a conjecture about whether the circula- the path, then no work is tion of F on C is positive, negative, or zero. path. b. Compute the circulation and interpret the result. d. The flux of a vector field 47. F = (y - x, x); C.r(1) = (2 cost, 2 sint), for 0 S t s 27 using a line integral. F= ( -xx) 52. Flying into a headwind An x increases in the eastward distance above the ground