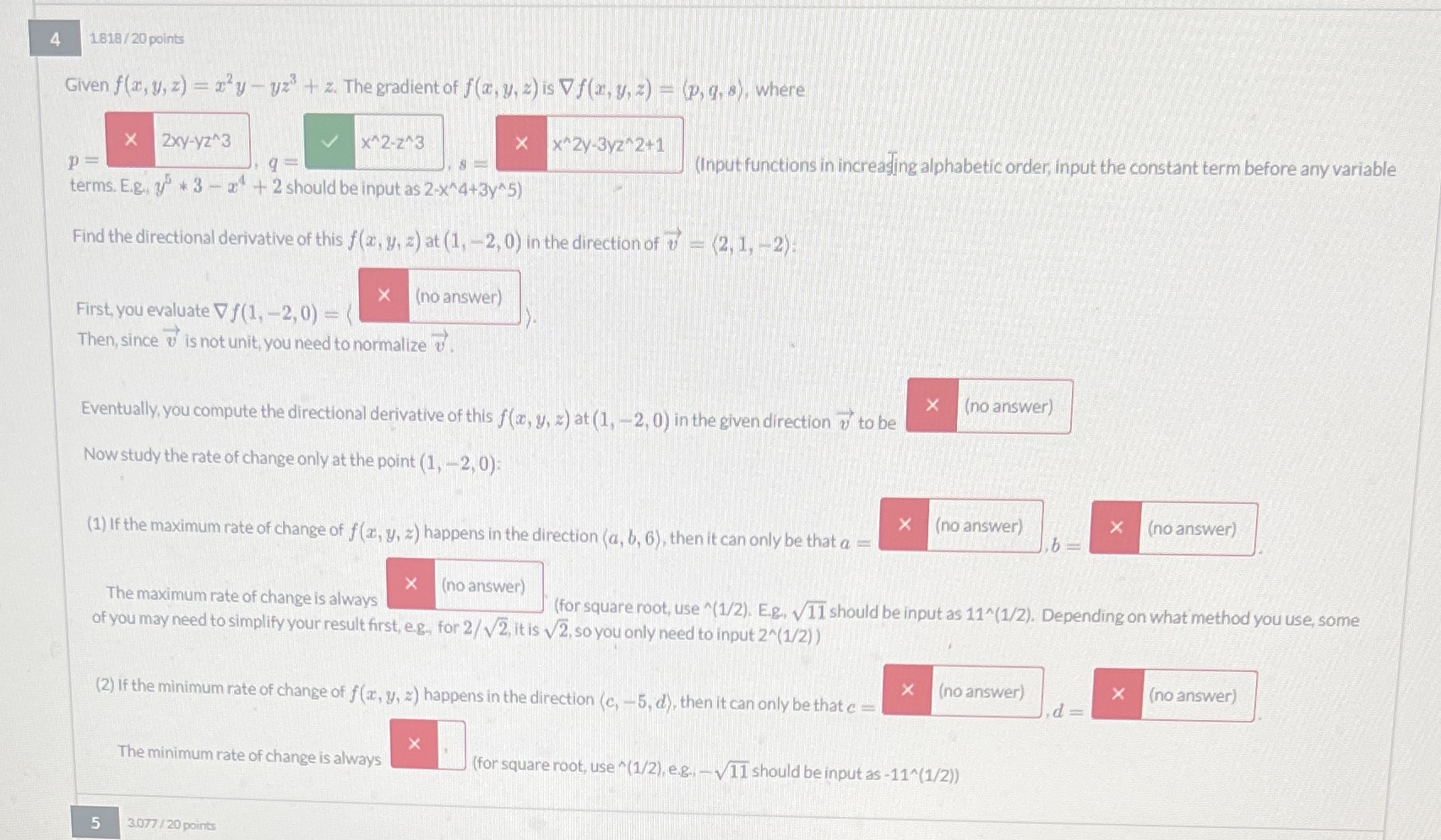
4 1818/20 points Given f(x, y, z) = ry-yz + z. The gradient of f(x, y, z) is Vf(x, y, z) = (p, q, 8), where X 2xy-yz^3 x^2-z^3 x^2y-3yz^2+1 P 9= (Input functions in increasing alphabetic order, input the constant term before any variable * terms. E.g. y 3-4 + 2 should be input as 2-x^4+3y^5) Find the directional derivative of this f(x, y, z) at (1,-2,0) in the direction of = (2,1,-2): First, you evaluate Vf(1, -2, 0) = (no answer) Then, since is not unit, you need to normalize. (no answer) Eventually, you compute the directional derivative of this f(x, y, z) at (1, -2, 0) in the given direction to be Now study the rate of change only at the point (1,-2,0): (no answer) (no answer) (1) If the maximum rate of change of f(x, y, z) happens in the direction (a, b, 6), then it can only be that a = ,b= (no answer) The maximum rate of change is always (for square root, use ^(1/2). Eg, 11 should be input as 11^(1/2). Depending on what method you use, some of you may need to simplify your result first, eg, for 2/2, it is 2, so you only need to input 2^(1/2)) (no answer) X (no answer) (2) If the minimum rate of change of f(x, y, z) happens in the direction (c, -5, d), then it can only be that c = d= The minimum rate of change is always (for square root, use ^(1/2), e.g., -11 should be input as -11^(1/2)) 5 3.077/20 points