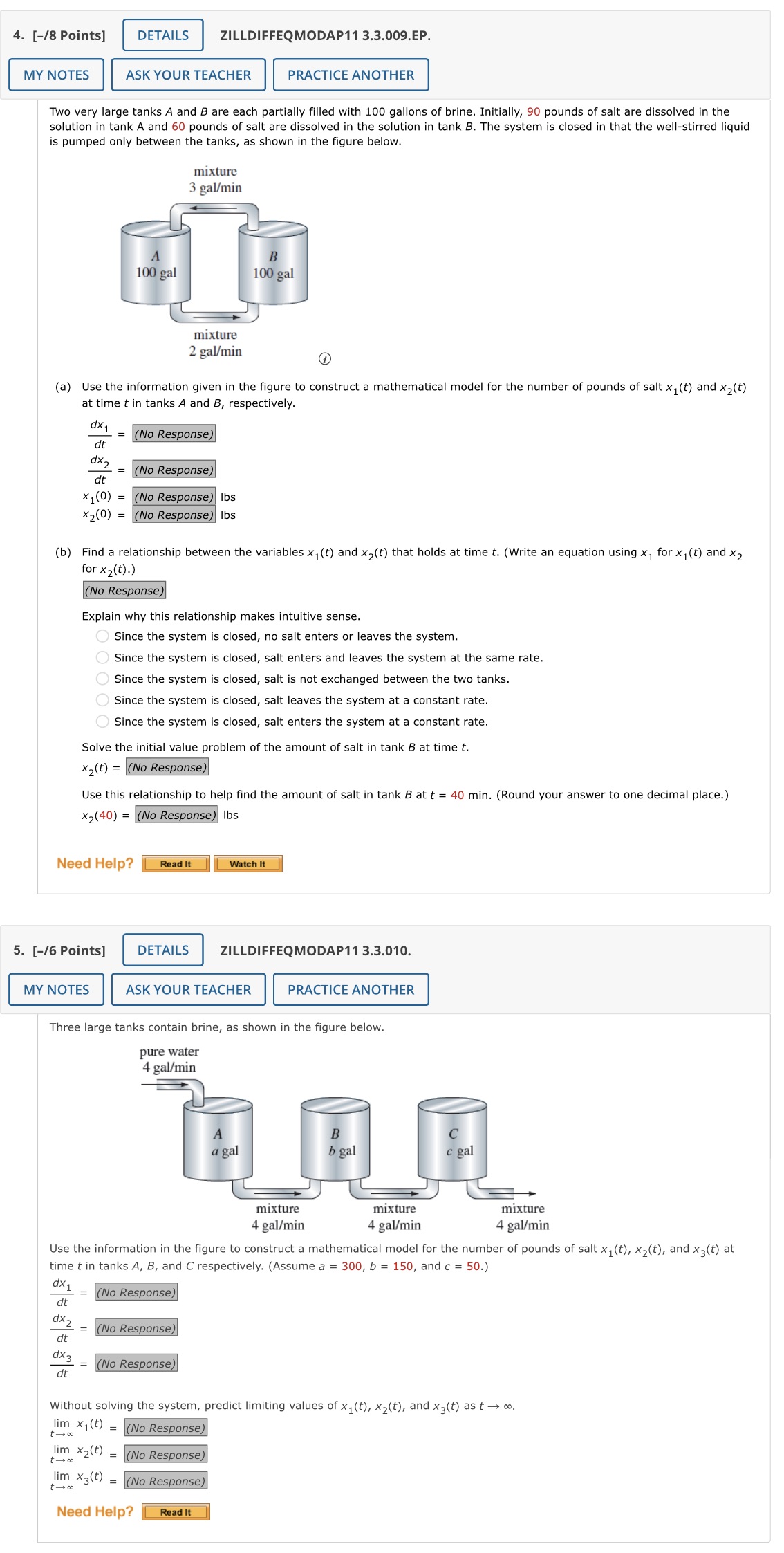
4. [-/8 Points] DETAILS ZILLDIFFEQMODAP11 3.3.009.EP. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Two very large tanks A and B are each partially filled with 100 gallons of brine. Initially, 90 pounds of salt are dissolved in the solution in tank A and 60 pounds of salt are dissolved in the solution in tank B. The system is closed in that the well-stirred liquid is pumped only between the tanks, as shown in the figure below. mixture 3 gal/min B 100 gal 100 gal mixture 2 gal/min (a) Use the information given in the figure to construct a mathematical model for the number of pounds of salt x, (t) and x2(t) at time t in tanks A and B, respectively. dx1 = (No Response) dt dx 2 _ dt = (No Response) *1(0) = (No Response) Ibs X2(0) = (No Response) Ibs (b) Find a relationship between the variables x, (t) and x2(t) that holds at time t. (Write an equation using x ] for x] (t) and x2 for x2(t). ) (No Response) Explain why this relationship makes intuitive sense. Since the system is closed, no salt enters or leaves the system. Since the system is closed, salt enters and leaves the system at the same rate. Since the system is closed, salt is not exchanged between the two tanks. Since the system is closed, salt leaves the system at a constant rate. Since the system is closed, salt enters the system at a constant rate. Solve the initial value problem of the amount of salt in tank B at time t. *2 (t) = (No Response) Use this relationship to help find the amount of salt in tank B at t = 40 min. (Round your answer to one decimal place.) X2(40) = (No Response) Ibs Need Help? Read It Watch It 5. [-/6 Points] DETAILS ZILLDIFFEQMODAP11 3.3.010. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Three large tanks contain brine, as shown in the figure below. pure water 4 gal/min B C a gal b gal c gal mixture mixture mixture 4 gal/min 4 gal/min 4 gal/min Use the information in the figure to construct a mathematical model for the number of pounds of salt x , (t), X2(t), and x3(t) at time t in tanks A, B, and C respectively. (Assume a = 300, b = 150, and c = 50.) ax 1 (No Response) dt ax 2 (No Response) dt dx 3 dt (No Response) Without solving the system, predict limiting values of x1 (t), X2(t), and x3(t) as t - co. t-+00 lim X1 (t) = (No Response) 1 -+ 20 lim X2(t) = (No Response) t -+ lim X3(t) = (No Response) Need Help? Read It