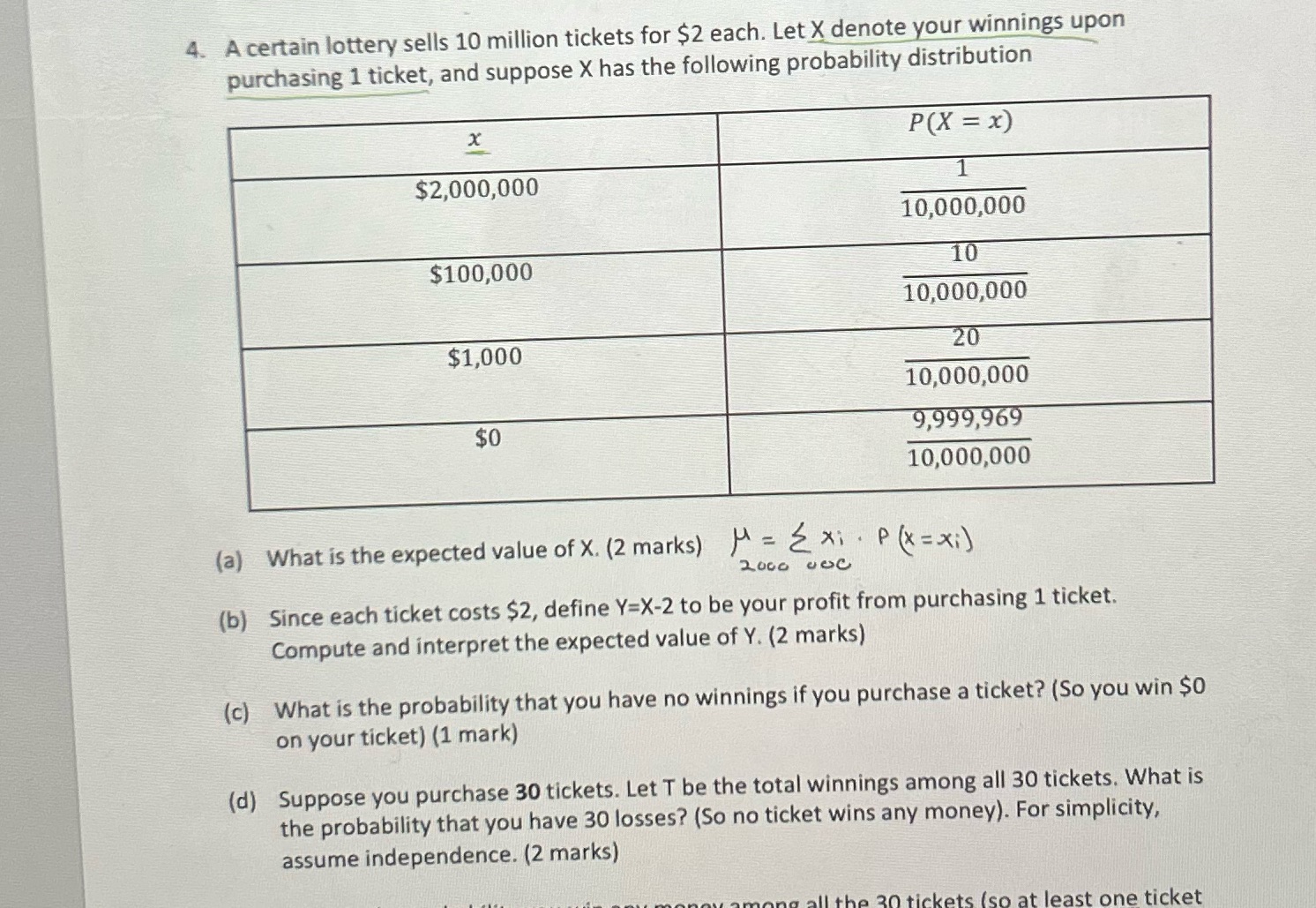
4. A certain lottery sells 10 million tickets for $2 each. Let X denote your winnings upon purchasing 1 ticket, and suppose X has the following probability distribution x $2,000,000 $100,000 $1,000 $0 (a) What is the expected value of X. (2 marks) = {x. 2000 ve P(X = x) 1 10,000,000 10 10,000,000 20 10,000,000 9,999,969 10,000,000 P (x = xi) (b) Since each ticket costs $2, define Y-X-2 to be your profit from purchasing 1 ticket. Compute and interpret the expected value of Y. (2 marks) (c) What is the probability that you have no winnings if you purchase a ticket? (So you win $0 on your ticket) (1 mark) (d) Suppose you purchase 30 tickets. Let T be the total winnings among all 30 tickets. What is the probability that you have 30 losses? (So no ticket wins any money). For simplicity, assume independence. (2 marks) ong all the 30 tickets (so at least one ticket