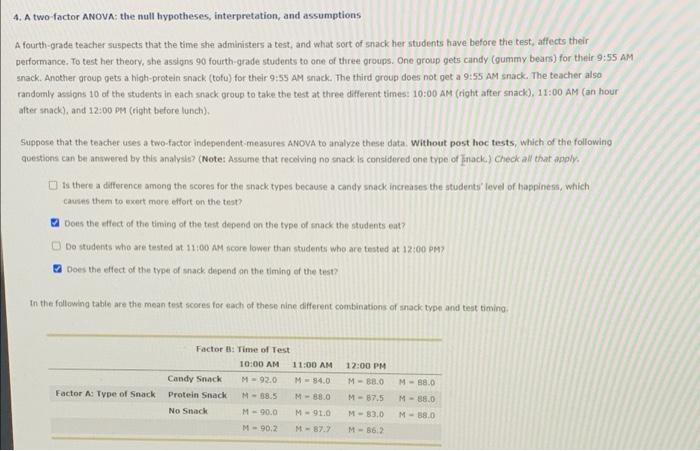
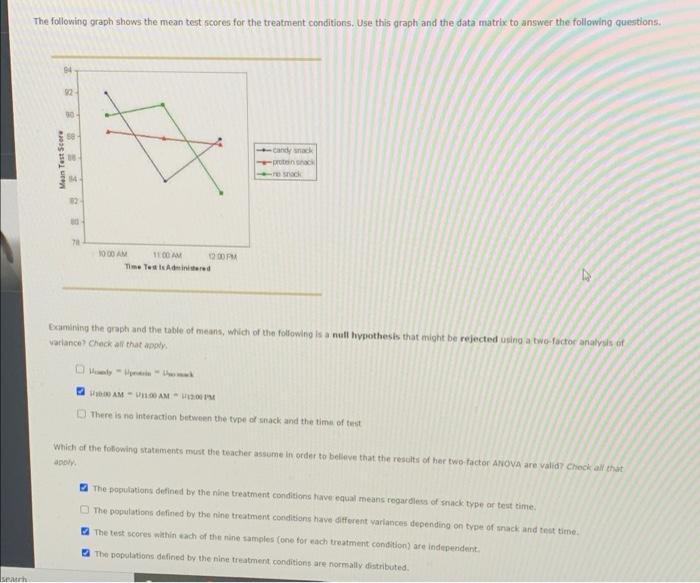
4. A two factor ANOVA: the null hypotheses, interpretation, and assumptions A fourth-grade teacher suspects that the time she administers a test, and what sort of snack her students have before the test, affects their performance. To test her theory, she assigns 90 fourth-grade students to one of three groups. One group gets candy (gummy bears) for their 9:55 AM snack. Another group gets a high protein snack (tofu) for their 9:55 AM snack. The third group does not get a 9:55 AM snack. The teacher also randomly assigns 10 of the students in each snack group to take the best at three different times: 10:00 AM (right after snack), 11:00 AM (an hour after snack), and 12:00 PM (right before lunch). Suppose that the teacher uses a two-factor independent measures ANOVA to analyze these data. Without post hoc tests, which of the following questions can be answered by this analysla? (Note: Assume that receiving no snack is considered one type of Inack.) Check all that apply. Is there a difference among the scores for the snack types because a candy snack increases the students level of happiness, which causes them to exert more effort on the test? Dous the effect of the timing of the test depend on the type of snack the students eat? Do students who are tested at 11:00 AM score lower than students who are tested at 12:00 PM Does the effect of the type of snack depend on the timing of the test? In the following table are the mean test scores for each of these nine different combinations of snack type and test timing Factor : Time of Test 10:00 AM 11:00 AM Candy Snack M - 92.0 M-94.0 Protein Snack M-58.5 M-880 No Snack M 90.0 M-910 12:00 PM M - BO Factor A: Type of Snack M - 8.0 M - 88.0 M-87,5 M-83.0 M-380 M-90.2 M-87. M-862 The following graph shows the mean test scores for the treatment conditions. Use this graph and the data matrix to answer the following questions. 30 Mein Test Score Candy pron ODAM 11.00 Time Te Administered Examining the graph and the table of means, which of the following is a nult hypothesis that might be rejected using a two-factor analysis of variance? Check all that apply WAM-AM There is no interaction between the type of snack and the time of test which of the following statements must the teacher assume in order to believe that the results of her two-factor ANOVA are valid? Check all that The populations defined by the nine treatment conditions ave equal means regardless of snack type or test time The populations defined by the nine treatment conditions have different variances depending on type of track and test time The test scores within each of the nine samples (one for each treatment condition) are independent The populations defined by the nine treatment conditions are normally distributed rh