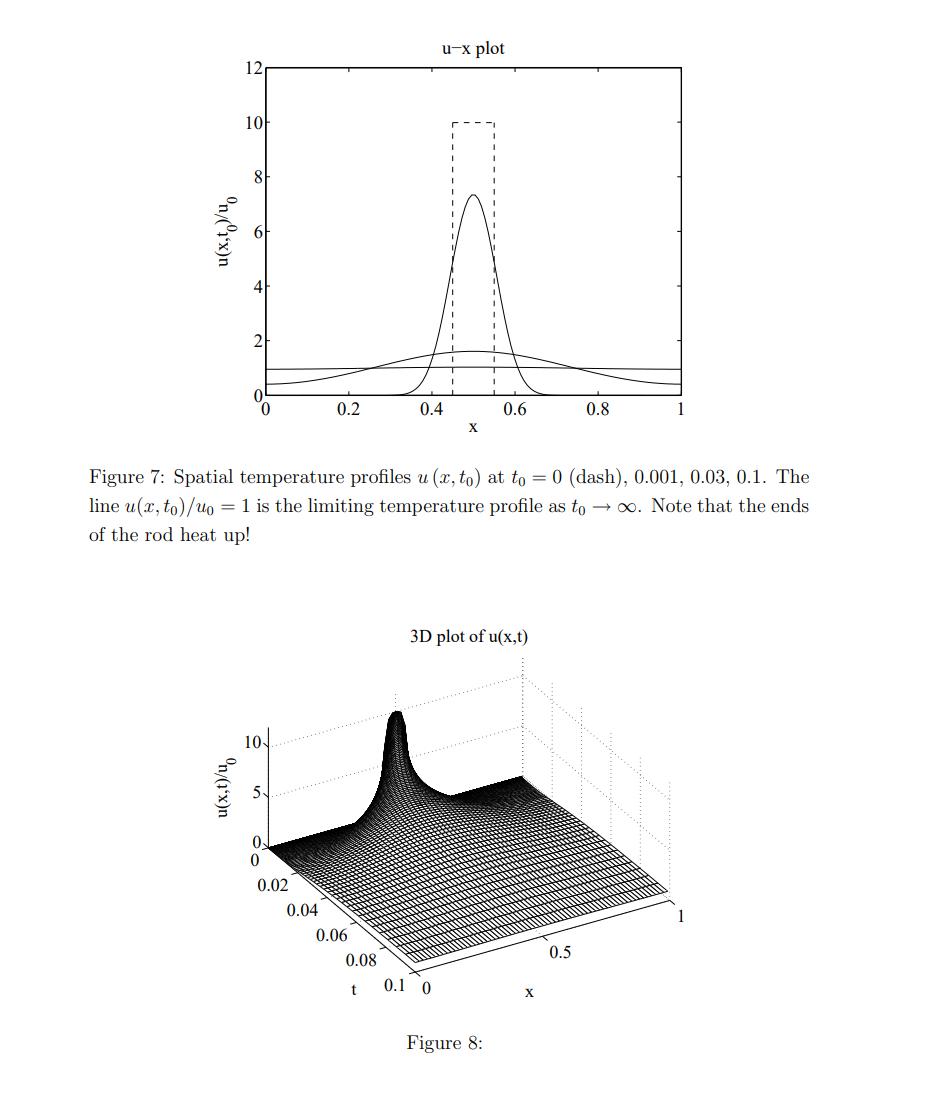
4. Consider the homogeneous heat problem with type III (mixed) BCs: du Ju u (x,0) = f(x) t x where t > 0, 0x 1 and f is a piecewise smooth function on [0, 1]. du x (0, t) = 0 = u(1, t); (a) Find the eigenvalues An and the eigenfunctions Xn (x) for this problem. Write the formal solution of the problem (a), and express the constant coefficients as integrals involving f (x). (b) Find a series solution in the case that f(x) = uo, uo a constant. Find an approximate solution good for large times. Sketch temperature profiles (u vs. x) for different times. n/1x)n 12 u(x,t)/u 10 21 0 10 0.02 0.2 0.04 0.06 Figure 7: Spatial temperature profiles u (x, to) at to = 0 (dash), 0.001, 0.03, 0.1. The line u(x, to)/uo 1 is the limiting temperature profile as to . Note that the ends of the rod heat up! 0.08 t u-x plot 0.4 X 0.1 0 0.6 3D plot of u(x,t) Figure 8: 0.8 0.5 1 0.1 0.08 0.06 0.04 0.02 0.5 0.25 0.2 Level curves u(x,t)=const 0.4 X 0.6 0.25 0.5 0.8 1 Figure 9: Level curves u (x, t) /uo = C for various values of the constant C. Numbers adjacent to curves indicate the value of C. The line segment (1-w)/2 x (1+w) /2 at t = 0 is the level curve with C = 1/w = 10. 00 (c) Evaluate limt- u(x, t) for the solution (a) when f (x) Pw (x) with P(x) defined in (5). Illustrate the solution qualitatively by sketching temperature profiles and level curves as in Problem 2(b). It is not necessary to find the complete formal solution. =