
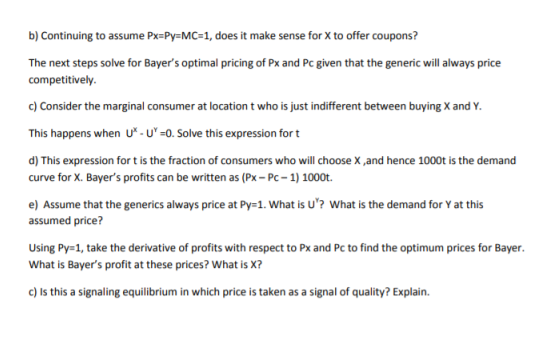
4. Extra credit problem. I could not figure out constant terms that made this model both solvable and feasible prices for Px and PC. You are welcome to try it, but when I solve it using Mathematica, (analytical software that is available for free from BU), it comes up with X=0, and Px-Pc=1. The reward to attracting people with a high price has to be concave (have diminishing returns) or an infinite amount of signaling happens. This one tries it with the log function. This question introduces a Hotelling type competition between Bayer and generics. Assume there are 1000 consumers to be divided up between the competing firms. One side is Bayer with its preferred brand X, the other side has a large number of competing generic firms offering Y at its marginal cost. Consumers choose Xor Y according to which gives them the most perceived utility. The assumption is that there are heterogeneous consumers distributed uniformly over t from 0 to 1, and the distance from their preferred optimum costs per unit distance from their origin. Bayer is located at 0, generics at 1. Bayer has the option of giving out free coupons that lower the price of its aspirin, which has a price effect but no effect on perceived quality of its brand. Using this notation we have: Utility of Bayer = V = 2+ log.(Px) - (Px-Pc) - 87 (4.1) Utility from generics = U'= 2 -Py- 6(1-t) (4.2) Note from this that Bayer differs from the generics in two ways. Its higher prices are perceived as a sign of quality, giving utility to its consumers, but at a diminishing rate since the log function is concave. Bayer also has the option of a coupon that lowers its price but not its perceived quality. a) If Bayer and the generics all set Px=Py=MC-1 and Pc-o, what is the share t of consumers that will choose Bayer? Assuming 1000 consumers in total, how many will choose Bayer? What are profits to Bayer and the generic firms? b) Continuing to assume Px=Py=MC-1, does it make sense for X to offer coupons? The next steps solve for Bayer's optimal pricing of Px and PC given that the generic will always price competitively. c) Consider the marginal consumer at location t who is just indifferent between buying X and Y. This happens when U* UY=0. Solve this expression fort d) This expression fort is the fraction of consumers who will choose X,and hence 1000t is the demand curve for X. Bayer's profits can be written as (Px-PC-1) 1000t. e) Assume that the generics always price at Py=1. What is u'? What is the demand for Yat this assumed price? Using Py=1, take the derivative of profits with respect to Px and Pc to find the optimum prices for Bayer. What is Bayer's profit at these prices? What is X? c) Is this a signaling equilibrium in which price is taken as a signal of quality? Explain. 4. Extra credit problem. I could not figure out constant terms that made this model both solvable and feasible prices for Px and PC. You are welcome to try it, but when I solve it using Mathematica, (analytical software that is available for free from BU), it comes up with X=0, and Px-Pc=1. The reward to attracting people with a high price has to be concave (have diminishing returns) or an infinite amount of signaling happens. This one tries it with the log function. This question introduces a Hotelling type competition between Bayer and generics. Assume there are 1000 consumers to be divided up between the competing firms. One side is Bayer with its preferred brand X, the other side has a large number of competing generic firms offering Y at its marginal cost. Consumers choose Xor Y according to which gives them the most perceived utility. The assumption is that there are heterogeneous consumers distributed uniformly over t from 0 to 1, and the distance from their preferred optimum costs per unit distance from their origin. Bayer is located at 0, generics at 1. Bayer has the option of giving out free coupons that lower the price of its aspirin, which has a price effect but no effect on perceived quality of its brand. Using this notation we have: Utility of Bayer = V = 2+ log.(Px) - (Px-Pc) - 87 (4.1) Utility from generics = U'= 2 -Py- 6(1-t) (4.2) Note from this that Bayer differs from the generics in two ways. Its higher prices are perceived as a sign of quality, giving utility to its consumers, but at a diminishing rate since the log function is concave. Bayer also has the option of a coupon that lowers its price but not its perceived quality. a) If Bayer and the generics all set Px=Py=MC-1 and Pc-o, what is the share t of consumers that will choose Bayer? Assuming 1000 consumers in total, how many will choose Bayer? What are profits to Bayer and the generic firms? b) Continuing to assume Px=Py=MC-1, does it make sense for X to offer coupons? The next steps solve for Bayer's optimal pricing of Px and PC given that the generic will always price competitively. c) Consider the marginal consumer at location t who is just indifferent between buying X and Y. This happens when U* UY=0. Solve this expression fort d) This expression fort is the fraction of consumers who will choose X,and hence 1000t is the demand curve for X. Bayer's profits can be written as (Px-PC-1) 1000t. e) Assume that the generics always price at Py=1. What is u'? What is the demand for Yat this assumed price? Using Py=1, take the derivative of profits with respect to Px and Pc to find the optimum prices for Bayer. What is Bayer's profit at these prices? What is X? c) Is this a signaling equilibrium in which price is taken as a signal of quality? Explain








