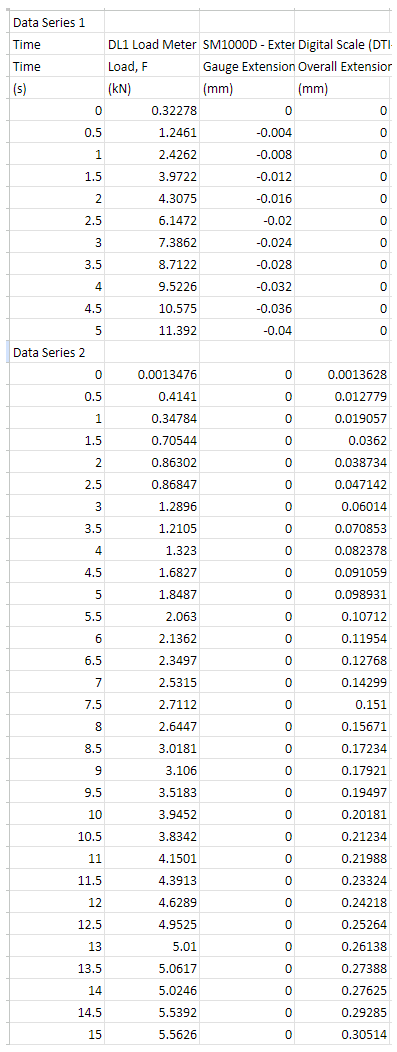
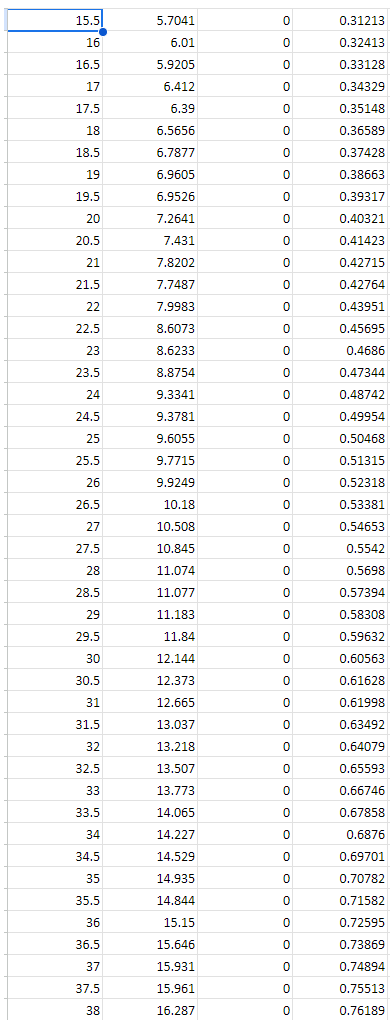
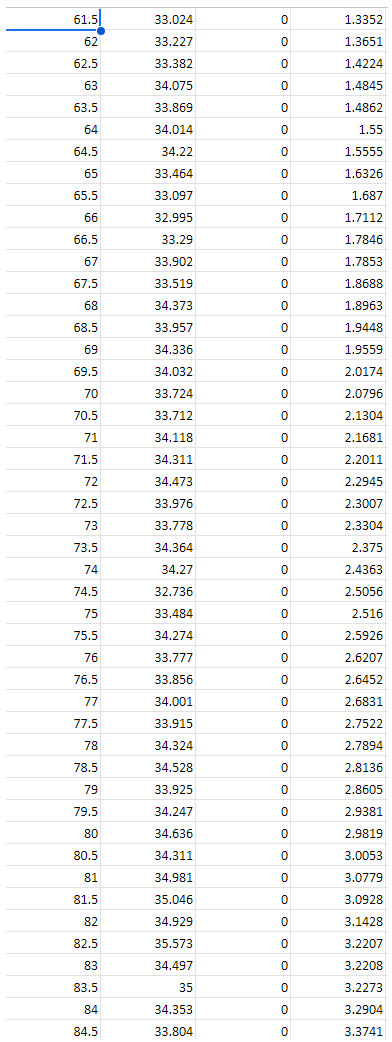
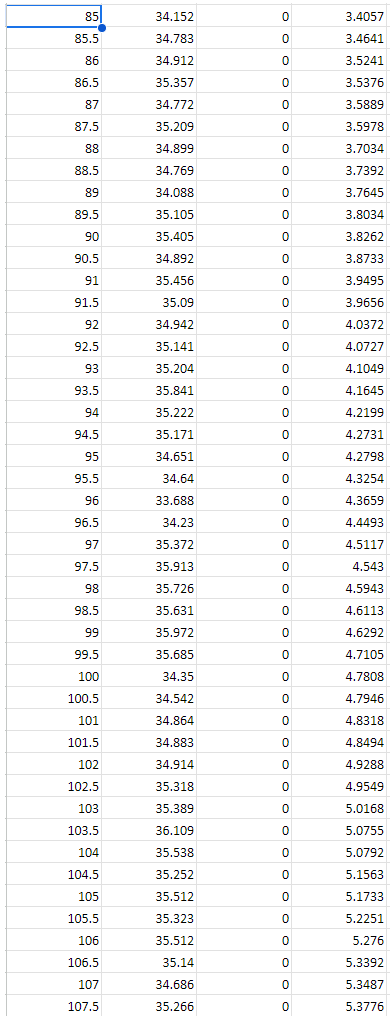
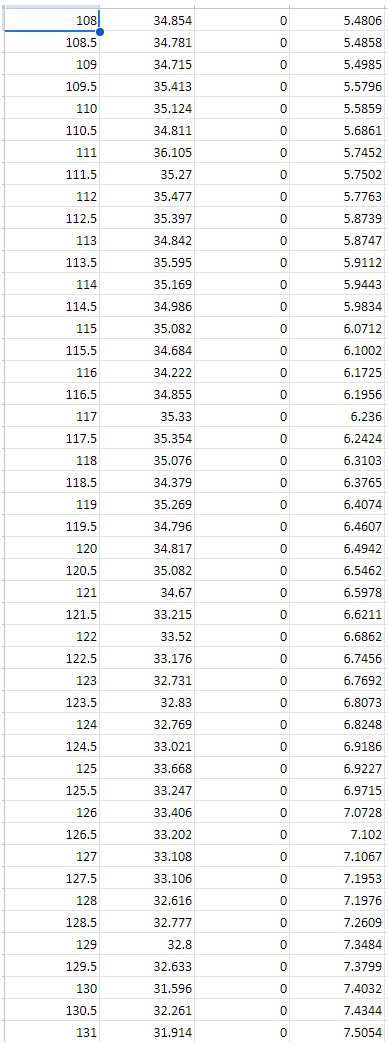
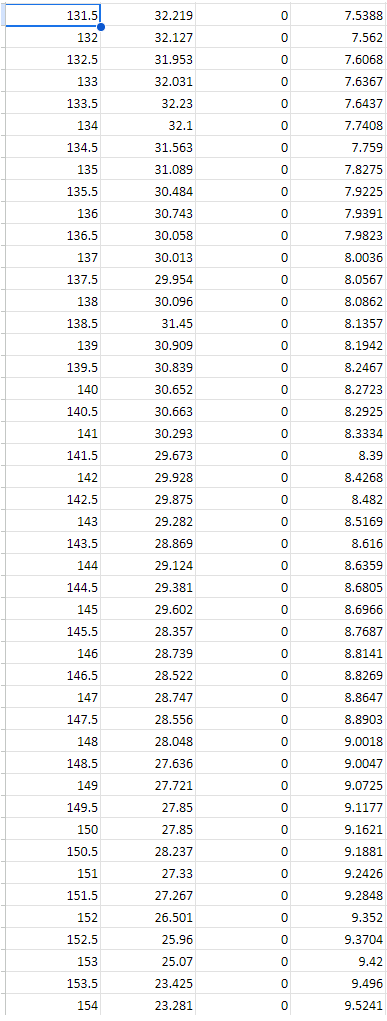
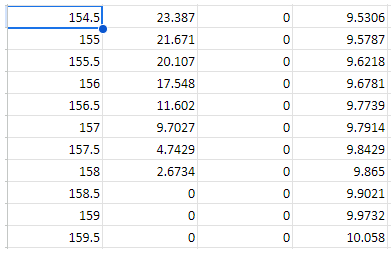
4. Part 1: Tensile testing The aim of the tensile test is to find the yield and ultimate tensile strengths and corresponding normal strains of the test material. This enables the prediction of the maximum shear stress that will be measured from the torsion test using failure theories. Data for the experiments can be found on SharePoint or Teams at Class Materials\Assignment Files\Assignment 1. Use the supplied dataset that matches with the LAST number in the 8 number string found beneath the QR code in your registered PSS booklet. The dataset is of a tensile test with a 1214 mild steel test specimen (dimensions can be found in Figure 1). Do the following tasks: 4.1. Analysis of results i. ii. iii. iv. V. vi. vii. viii. Plot graph(s) of the raw supplied data obtained from the tensile testing experiment. You should present the force vs. displacement relationship for both the extensometer (measured across a gauge length of 50 mm) and digital scale (measured across the loaded length of the specimen). Convert the raw supplied data to normal stress and normal strain &. You may need to adjust the data points to account for improper zeroing or other errors. The procedure should be clearly described and a fully worked example calculation should be given. Plot a graph of stress (vertical axis) against strain & (horizontal axis) using the extensometer data set. Calculate the Young's modulus E of the material using the extensometer data set. The procedure should be clearly described. Plot a graph of stress (vertical axis) against strain & (horizontal axis) using the digital scale data set. On your digital scale data set plot, mark the yield point using the 0.2% offset yield strength. The 0.2% offset yield strength is defined as the stress that will cause a permanent plastic strain deformation of 0.2%. Also present the value in writing. Mark the ultimate tensile stress on your plot. Also present the value in writing. Estimate the shear yield stress for a purely torsional loading using the failure theories in Section 3. 1. Introduction This assignment involves the analysis of data from two testings, namely tension and torsion tests. The tension test aims to identify the principles of tension testing and to interpret the experimental results of the provided materials when they failed under tension. Students will investigate the relationships between applied load, displacement, Young's modulus, yield strength and normal strain. 172 16. 140 83 R1.6 R1.5 All Dimensions in mm Figure 1. Dimensions of the tensile specimen The torsion test aims to identify the mechanical properties of a cylindrical specimen under angular motion. The test will require students to quantitatively investigate the relationships between torque and the angle of twist, modulus of rigidity (shear modulus), yield shear strength and shear strain. 140 mm 76 mm parallel Nominal 6 mm diameter Figure 2. Dimensions of the torsion specimen 11.3 mm across flats or 12 mm across flats 2. Fundamental theory This section shows the fundamental theory and equations used for calculations in the forthcoming experiments. 2.1. Normal stress and strain, and Young's Modulus Normal stress is the ratio of normal force to the cross-sectional area. It is found by: F A Normal strain is the change in length of a material over its original length. It is found by: = AL L (1) (2) Young's Modulus is the ratio of the normal stress divided by the normal strain on a material. It is a measure of the stiffness of a material. It is found by: E= E (3) 2.2. Modulus of Rigidity or Shear Modulus (G) The shear modulus, or modulus of rigidity, is a measure of the rigidity of the material when in 'shear' - when it is twisting. It is a ratio of the shear stress and the shear strain of the material: G= I (4) Both formulae (3) and (4) only describe the material behaviour when it is stressed within its elastic region. 2.3. Polar Moment of Inertia (J) The polar moment of inertia is representative of a shaft or beam's resistance to being distorted by torsion. The equation below describes the polar moment of inertia for a circular cross-section rod or specimen. A higher polar moment of inertia (J) indicates that the rod or specimen deforms less than a rod with a lower polar moment of inertia. The diameter (D) of the beam determines polar moment of inertia (J): D' J 32 The general equation for the torque in a beam or specimen is: T GO J = (5) (6) 2.4. Torque (T) Force (F) Torque Arm Known test length Angle of twist (0) 1 Diameter of specimen (D) Figure 3. Torque (twisting force) The twisting force (torque) at the end of a specimen is equal to the moment created by a force on the torque arm. This torque is calculated by: 2.5. Shear Stress (t) and Shear Strain (y) T=Fx Torque Arm Length The theoretical shear stress on the surface of a solid circular bar is: (7) TD 2J The theoretical shear strain on the surface of a solid circular bar is: 2.6. Notation 10 y === G 1 Symbol Description Units A Area m M Applied moment Nm F Force N L Total length of a specimen m 1 Gauge length m T Torque Nm J Polar moment of inertia m G Shear modulus Nm D Diameter of specimen m r Radius of specimen m Shear stress Nm V Shear strain Radians 0 Angle of twist Radians Normal stress Nm E Young's modulus Nm E Normal strain mm/mm (8) (9) 3. Failure theory for ductile materials When an engineer is faced with the problem of design using a specific material, it becomes important to place an upper limit on the state of stress that defines the material's failure. If the material is ductile, failure is usually specified by the initiation of yielding. A yield criterion is a hypothesis defining the limit of elasticity in a material and the onset of plastic deformation under any possible combination of stresses. Students are strongly recommended to refer to p. 524-527 of Mechanics of Materials 9th ed. by R. C. Hibbeler. Torsion failures are different from failures under tension and cause negligible elongation or deformation. The characteristic of the fracture surface under torsion is related to the state of stress at the element on the specimen surface, which is shown in Figure 4. The maximum shear stresses exist along two planes, which are perpendicular to each other. One is perpendicular to the longitudinal (x) axis and another is aligned parallel to the longitudinal (x) axis, as shown in Figure 4. The principal stresses and 3 are inclined at 45 to the longitudinal axis and have their magnitudes equal to those of the shear stresses. The principal stress is tensile while the principal stress 3 is compressive. The intermediate stress 2 is zero under torsion. max Tmx Figure 4. State of stresses in torsion (Dieter, G. E. Mechanical metallurgy, 1988, McGraw-Hill) The maximum-shear-stress theory (Tresca yield criterion) can be used to predict the failure stress of a ductile material subjected to any type of loading. The theory states that yielding of the material begins when the absolute maximum shear stress in the material reaches the shear stress that causes the same material to yield when it is subjected only to axial tension. Therefore, to avoid failure, it is required that as in the material must be less than or max equal to 2 + where is the yield stress determined from a simple tension test. The maximum-distortion-energy theory (von Mises failure criterion) explains that yielding in a ductile material occurs when the distortion energy per unit volume of the material equals or exceeds the distortion energy per unit volume of the same material when it is subjected to yielding in a simple tension test. The value of von Mises stress needed to cause yielding can be determined from the tensile yield stress y. The shear yield stress can similarly be found by inserting the principal stresses corresponding to a state of pure shear. Therefore, to avoid failure, it is required that r abs max in the material must be less than or equal to Data Series 1 Time DL1 Load Meter SM1000D - Exter Digital Scale (DTI Load, F Gauge Extension Overall Extensior Time (s) (kN) (mm) (mm) 0 0.32278 0 0 0.5 1.2461 -0.004 0 1 2.4262 -0.008 0 1.5 3.9722 -0.012 0 2 4.3075 -0.016 0 2.5 6.1472 -0.02 0 3 7.3862 -0.024 0 3.5 8.7122 -0.028 0 4 9.5226 -0.032 0 4.5 10.575 -0.036 0 5 11.392 -0.04 0 Data Series 2 0 0.0013476 0 0.0013628 0.5 0.4141 0 0.012779 1 0.34784 0 0.019057 1.5 0.70544 0 0.0362 2 0.86302 0 0.038734 2.5 0.86847 0 0.047142 3 1.2896 0 0.06014 3.5 1.2105 0 0.070853 4 1.323 0 0.082378 4.5 1.6827 0 0.091059 5 1.8487 0 0.098931 5.5 2.063 0 0.10712 6 2.1362 0 0.11954 6.5 2.3497 0 0.12768 7 2.5315 0 0.14299 7.5 2.7112 0 0.151 8 2.6447 0 0.15671 8.5 3.0181 0 0.17234 9 3.106 0 0.17921 9.5 3.5183 0 0.19497 10 3.9452 0 0.20181 10.5 3.8342 0 0.21234 11 4.1501 0 0.21988 11.5 4.3913 0 0.23324 12 4.6289 0 0.24218 12.5 4.9525 0 0.25264 13 5.01 0 0.26138 13.5 5.0617 0 0.27388 14 5.0246 0 0.27625 14.5 5.5392 0 0.29285 15 5.5626 0 0.30514 15.5 5.7041 0 0.31213 16 6.01 0 0.32413 16.5 5.9205 0 0.33128 17 6.412 0 0.34329 17.5 6.39 0 0.35148 18 6.5656 0 0.36589 18.5 6.7877 0 0.37428 19 6.9605 0 0.38663 19.5 6.9526 0 0.39317 20 7.2641 0 0.40321 20.5 7.431 0 0.41423 21 7.8202 0 0.42715 21.5 7.7487 0 0.42764 22 7.9983 0 0.43951 22.5 8.6073 0 0.45695 23 8.6233 0 0.4686 23.5 8.8754 0 0.47344 24 9.3341 0 0.48742 24.5 9.3781 0 0.49954 25 9.6055 0 0.50468 25.5 9.7715 0 0.51315 26 9.9249 0 0.52318 26.5 10.18 0 0.53381 27 10.508 0 0.54653 27.5 10.845 0 0.5542 28 11.074 0 0.5698 28.5 11.077 0 0.57394 29 11.183 0 0.58308 29.5 11.84 0 0.59632 30 12.144 0 0.60563 30.5 12.373 0 0.61628 31 12.665 0 0.61998 31.5 13.037 0 0.63492 32 13.218 0 0.64079 32.5 13.507 0 0.65593 33 13.773 0 0.66746 33.5 14.065 0 0.67858 34 14.227 0 0.6876 34.5 14.529 0 0.69701 35 14.935 0 0.70782 35.5 14.844 0 0.71582 36 15.15 0 0.72595 36.5 15.646 0 0.73869 37 15.931 0 0.74894 37.5 15.961 0 0.75513 38 16.287 0 0.76189 38 16.287 0 0.76189 38.5 16.604 0 0.77073 39 16.888 0 0.7825 39.5 17.011 0 0.79414 40 17.506 0 0.80784 40.5 17.705 0 0.81487 41 18.11 0 0.82668 41.5 18.423 0 0.8379 42 18.586 0 0.84359 42.5 19.222 0 0.85502 43 19.319 0 0.86535 43.5 19.642 0 0.87531 44 20.024 0 0.8863 44.5 20.244 0 0.89945 45 20.531 0 0.90629 45.5 21.133 0 0.91938 46 21.429 0 0.92858 46.5 21.599 0 0.93829 47 22.219 0 0.95034 47.5 22.511 0 0.96333 48 22.793 0 0.97174 48.5 22.866 0 0.97419 49 23.282 0 0.98956 49.5 23.337 0 0.9952 50 23.778 0 1.0034 50.5 24.048 0 1.0155 51 24.453 0 1.0231 51.5 24.93 0 1.0358 52 25.48 0 1.0521 52.5 25.503 0 1.0576 53 26.245 0 1.0756 53.5 26.22 0 1.08 54 26.707 0 1.0916 54.5 26.949 0 1.0988 55 27.324 0 1.1085 55.5 27.212 0 1.1174 56 27.876 0 1.1298 56.5 27.967 0 1.1358 57 28.358 0 1.1475 57.5 28.632 0 1.157 58 29.163 0 1.1702 58.5 29.57 0 1.1836 59 29.919 0 1.1953 59.5 29.936 0 1.1956 60 30.607 0 1.2087 60.5 31.126 0 1.2279 61 32.147 0 1.2614 61.5 33.024 0 1.3352 62 33.227 0 1.3651 62.5 33.382 0 1.4224 63 34.075 0 1.4845 63.5 33.869 0 1.4862 64 34.014 0 1.55 64.5 34.22 0 1.5555 65 33.464 0 1.6326 65.5 33.097 0 1.687 66 32.995 0 1.7112 66.5 33.29 0 1.7846 67 33.902 0 1.7853 67.5 33.519 0 1.8688 68 34.373 0 1.8963 68.5 33.957 0 1.9448 69 34.336 0 1.9559 69.5 34.032 0 2.0174 70 33.724 0 2.0796 70.5 33.712 0 2.1304 71 34.118 0 2.1681 71.5 34.311 0 2.2011 72 34.473 0 2.2945 72.5 33.976 0 2.3007 73 33.778 0 2.3304 73.5 34.364 0 2.375 74 34.27 0 2.4363 74.5 32.736 0 2.5056 75 33.484 0 2.516 75.5 34.274 0 2.5926 76 33.777 0 2.6207 76.5 33.856 0 2.6452 77 34.001 0 2.6831 77.5 33.915 0 2.7522 78 34.324 0 2.7894 78.5 34.528 0 2.8136 79 33.925 0 2.8605 79.5 34.247 0 2.9381 80 34.636 0 2.9819 80.5 34.311 0 3.0053 81 34.981 0 3.0779 81.5 35.046 0 3.0928 82 34.929 0 3.1428 82.5 35.573 0 3.2207 83 34.497 0 3.2208 83.5 35 0 3.2273 84 34.353 0 3.2904 84.5 33.804 0 3.3741 85 34.152 0 3.4057 85.5 34.783 0 3.4641 86 34.912 0 3.5241 86.5 35.357 0 3.5376 87 34.772 0 3.5889 87.5 35.209 0 3.5978 88 34.899 0 3.7034 88.5 34.769 0 3.7392 89 34.088 0 3.7645 89.5 35.105 0 3.8034 90 35.405 0 3.8262 90.5 34.892 0 3.8733 91 35.456 0 3.9495 91.5 35.09 0 3.9656 92 34.942 0 4.0372 92.5 35.141 0 4.0727 93 35.204 0 4.1049 93.5 35.841 0 4.1645 94 35.222 0 4.2199 94.5 35.171 0 4.2731 95 34.651 0 4.2798 95.5 34.64 0 4.3254 96 33.688 0 4.3659 96.5 34.23 0 4.4493 97 35.372 0 4.5117 97.5 35.913 0 4.543 98 35.726 0 4.5943 98.5 35.631 0 4.6113 99 35.972 0 4.6292 99.5 35.685 0 4.7105 100 34.35 0 4.7808 100.5 34.542 0 4.7946 101 34.864 0 4.8318 101.5 34.883 0 4.8494 102 34.914 0 4.9288 102.5 35.318 0 4.9549 103 35.389 0 5.0168 103.5 36.109 0 5.0755 104 35.538 0 5.0792 104.5 35.252 0 5.1563 105 35.512 0 5.1733 105.5 35.323 0 5.2251 106 35.512 0 5.276 106.5 35.14 0 5.3392 107 34.686 0 5.3487 107.5 35.266 0 5.3776 108 34.854 0 5.4806 108.5 34.781 0 5.4858 109 34.715 0 5.4985 109.5 35.413 0 5.5796 110 35.124 0 5.5859 110.5 34.811 0 5.6861 111 36.105 0 5.7452 111.5 35.27 0 5.7502 112 35.477 0 5.7763 112.5 35.397 0 5.8739 113 34.842 0 5.8747 113.5 35.595 0 5.9112 114 35.169 0 5.9443 114.5 34.986 0 5.9834 115 35.082 0 6.0712 115.5 34.684 0 6.1002 116 34.222 0 6.1725 116.5 34.855 0 6.1956 117 35.33 0 6.236 117.5 35.354 0 6.2424 118 35.076 0 6.3103 118.5 34.379 0 6.3765 119 35.269 0 6.4074 119.5 34.796 0 6.4607 120 34.817 0 6.4942 120.5 35.082 0 6.5462 121 34.67 0 6.5978 121.5 33.215 0 6.6211 122 33.52 0 6.6862 122.5 33.176 0 6.7456 123 32.731 0 6.7692 123.5 32.83 0 6.8073 124 32.769 0 6.8248 124.5 33.021 0 6.9186 125 33.668 0 6.9227 125.5 33.247 0 6.9715 126 33.406 0 7.0728 126.5 33.202 0 7.102 127 33.108 0 7.1067 127.5 33.106 0 7.1953 128 32.616 0 7.1976 128.5 32.777 0 7.2609 129 32.8 0 7.3484 129.5 32.633 0 7.3799 130 31.596 0 7.4032 130.5 32.261 0 7.4344 131 31.914 0 7.5054 131.5 32.219 0 7.5388 132 32.127 0 7.562 132.5 31.953 0 7.6068 133 32.031 0 7.6367 133.5 32.23 0 7.6437 134 32.1 0 7.7408 134.5 31.563 0 7.759 135 31.089 0 7.8275 135.5 30.484 0 7.9225 136 30.743 0 7.9391 136.5 30.058 0 7.9823 137 30.013 0 8.0036 137.5 29.954 0 8.0567 138 30.096 0 8.0862 138.5 31.45 0 8.1357 139 30.909 0 8.1942 139.5 30.839 0 8.2467 140 30.652 0 8.2723 140.5 30.663 0 8.2925 141 30.293 0 8.3334 141.5 29.673 0 8.39 142 29.928 0 8.4268 142.5 29.875 0 8.482 143 29.282 0 8.5169 143.5 28.869 0 8.616 144 29.124 0 8.6359 144.5 29.381 0 8.6805 145 29.602 0 8.6966 145.5 28.357 0 8.7687 146 28.739 0 8.8141 146.5 28.522 0 8.8269 147 28.747 0 8.8647 147.5 28.556 0 8.8903 148 28.048 0 9.0018 148.5 27.636 0 9.0047 149 27.721 0 9.0725 149.5 27.85 0 9.1177 150 27.85 0 9.1621 150.5 28.237 0 9.1881 151 27.33 0 9.2426 151.5 27.267 0 9.2848 152 26.501 0 9.352 152.5 25.96 0 9.3704 153 25.07 0 9.42 153.5 23.425 0 9.496 154 23.281 0 9.5241 154.5 23.387 0 9.5306 155 21.671 0 9.5787 155.5 20.107 0 9.6218 156 17.548 0 9.6781 156.5 11.602 0 9.7739 157 9.7027 0 9.7914 157.5 4.7429 0 9.8429 158 2.6734 0 9.865 158.5 0 0 9.9021 159 0 0 9.9732 159.5 0 0 10.058