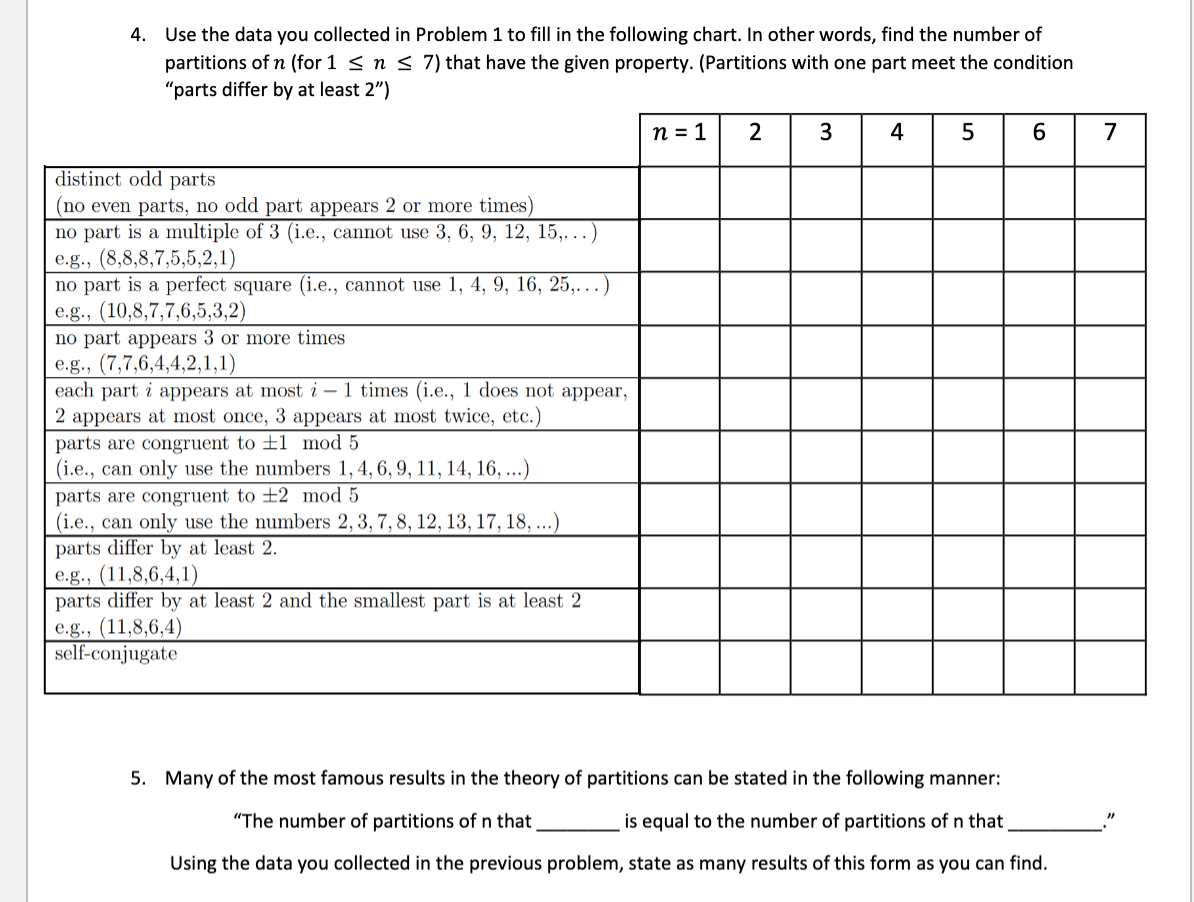
4. Use the data you collected in Problem 1 to fill in the following chart. In other words, find the number of partitions of n (for 1 sn s 7) that have the given property. (Partitions with one part meet the condition "parts differ by at least 2") n=1 2 3 4 5 6 distinct odd parts (no even parts, no odd part appears 2 or more times) no part is a multiple of 3 (i.e., cannot use 3, 6, 9, 12, 15,...) e.g., (8,8,8,7,5,5,2,1) no part is a perfect square (i.e., cannot use 1, 4, 9, 16, 25,...) e.g., (10,8,7,7,6,5,3,2) no part appears 3 or more times e.g., (7,7,6,4,4,2,1,1) each part i appears at most i - 1 times i.e., 1 does not appear, 2 appears at most once, 3 appears at most twice, etc.) parts are congruent to +1 mod 5 (i.e., can only use the numbers 1, 4, 6, 9, 11, 14, 16, ...) parts are congruent to +2 mod 5 (i.e., can only use the numbers 2, 3, 7, 8, 12, 13, 17, 18, ...) parts differ by at least 2. e.g., (11,8,6,4,1) parts differ by at least 2 and the smallest part is at least 2 e.g., (11,8,6,4) self-conjugate 5. Many of the most famous results in the theory of partitions can be stated in the following manner: "The number of partitions of n that is equal to the number of partitions of n that Using the data you collected in the previous problem, state as many results of this form as you can find. 4. Use the data you collected in Problem 1 to fill in the following chart. In other words, find the number of partitions of n (for 1 sn s 7) that have the given property. (Partitions with one part meet the condition "parts differ by at least 2") n=1 2 3 4 5 6 distinct odd parts (no even parts, no odd part appears 2 or more times) no part is a multiple of 3 (i.e., cannot use 3, 6, 9, 12, 15,...) e.g., (8,8,8,7,5,5,2,1) no part is a perfect square (i.e., cannot use 1, 4, 9, 16, 25,...) e.g., (10,8,7,7,6,5,3,2) no part appears 3 or more times e.g., (7,7,6,4,4,2,1,1) each part i appears at most i - 1 times i.e., 1 does not appear, 2 appears at most once, 3 appears at most twice, etc.) parts are congruent to +1 mod 5 (i.e., can only use the numbers 1, 4, 6, 9, 11, 14, 16, ...) parts are congruent to +2 mod 5 (i.e., can only use the numbers 2, 3, 7, 8, 12, 13, 17, 18, ...) parts differ by at least 2. e.g., (11,8,6,4,1) parts differ by at least 2 and the smallest part is at least 2 e.g., (11,8,6,4) self-conjugate 5. Many of the most famous results in the theory of partitions can be stated in the following manner: "The number of partitions of n that is equal to the number of partitions of n that Using the data you collected in the previous problem, state as many results of this form as you can find