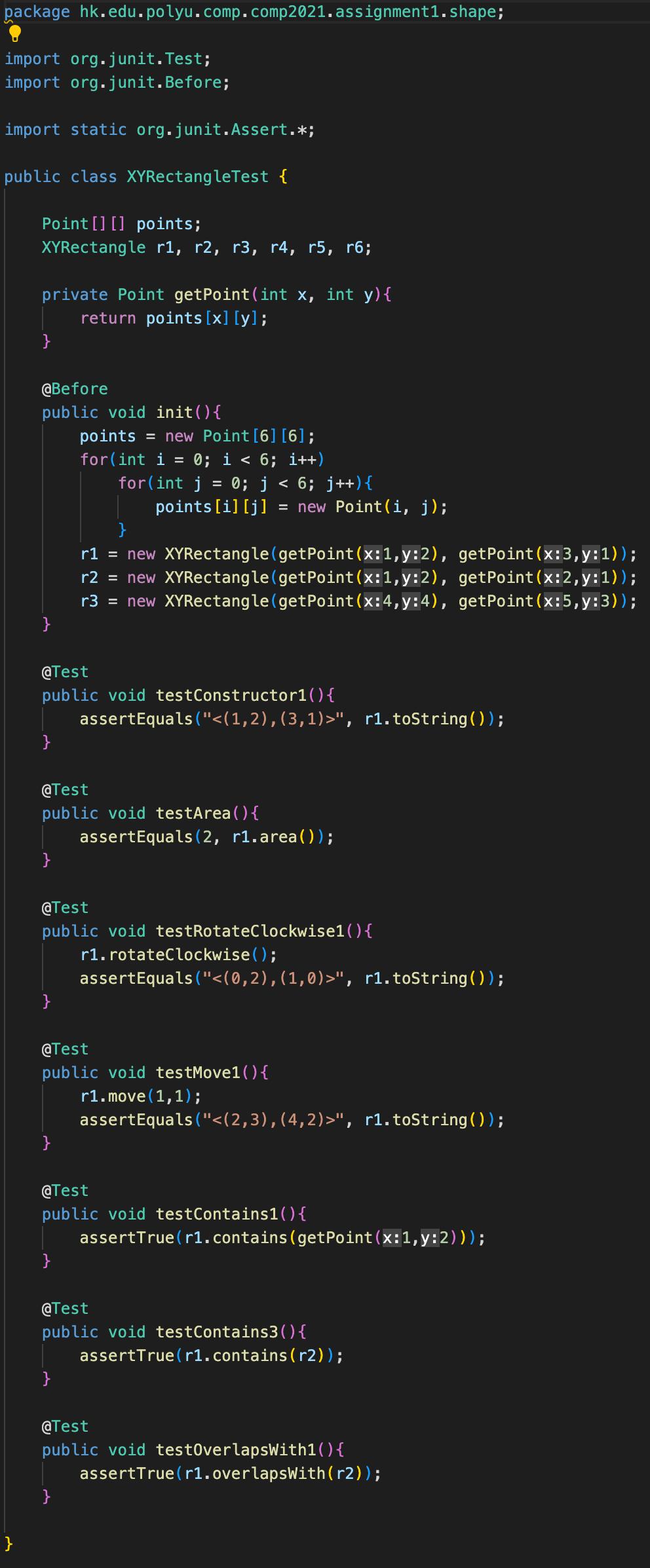
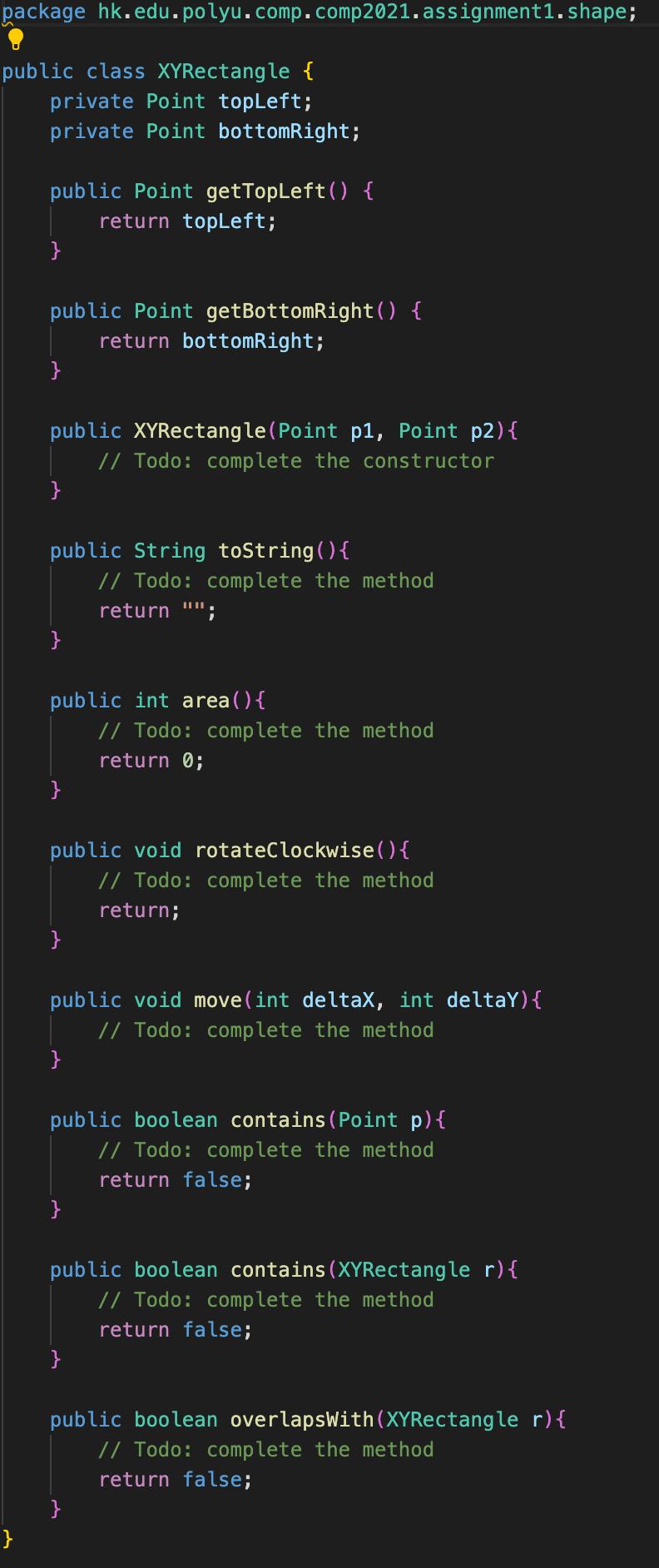
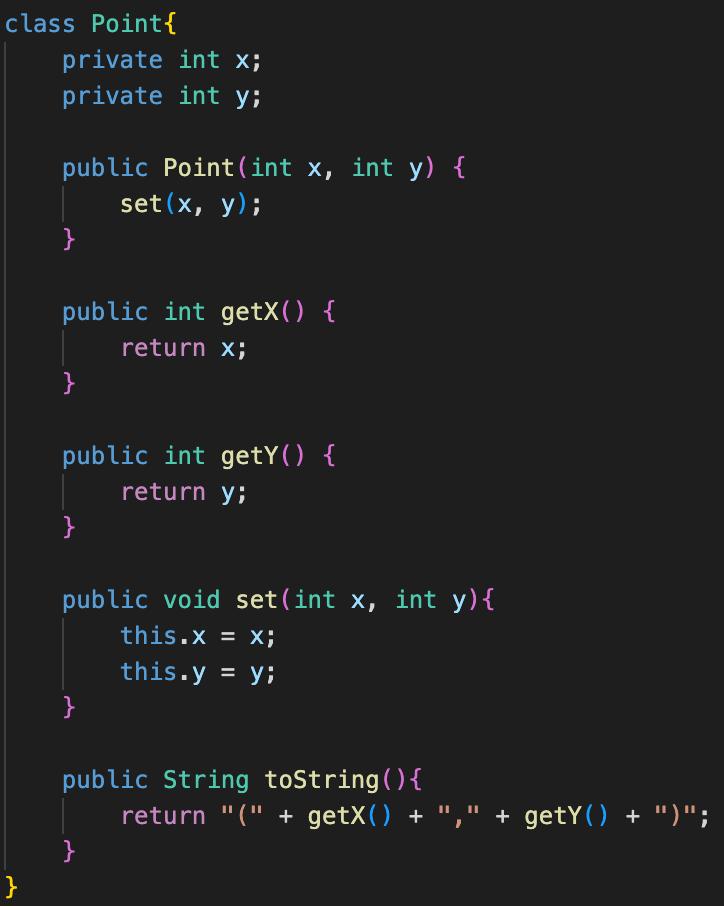
4. XY-Rectangle (20 points) A point P in a Cartesian coordinate system can be denoted using its x-coordinate and y-coordinate as (Xp,yp), and an xy-rectangle, i.e., a rectangle with its four sides in parallel or overlapping with the x- and y-axes, can be represented using its top-left vertex Pul and bottom-right vertex Pbr as . For example, xy- rectangle R in Figure 1 (in solid line) can be represented as , while xy-rectangle R2 (in dotted line) can be represented as . Given class Point as defined in XYRectangle.java, please complete class XYRectangle so that each XYRectangle object represents a valid xy-rectangle and supports the following operations: y P1 R2 R1 P4 P2 Figure 1. Two xy-rectangles. 1. A constructor that takes two points as arguments and initializes the newly created xy- rectangle in such a way that the line segment between the two points forms a diagonal of the rectangle; You may assume that the line passing both argument points always intersects with both the x and the y axis. 2. A method toString that returns a String representation of the xy-rectangle in the form , where a point P with coordinates Px and Py is denoted as (Px,Py). For example, given an xy-rectangle with the top-left and bottom-right vertexes at positions (2,3) and (4,1), invoking toString on the xy-rectangle will return " ". 3. A method area that takes no argument and returns the area of the xy-rectangle. 4. A method rotate Clockwise that takes no argument and rotates the current xy-rectangle clockwise by 90 degrees around its top-left vertex; For example, xy-rectangle R in Figure 1 will be at the position of R2 after the method is invoked on R1. 5. A method move that takes two arguments deltax and deltaY and moves the xy-rectangle horizontally by deltax and vertically by deltaY. 6. A method contains that takes a point P as the argument and returns true if and only if the point is within or on the border of the xy-rectangle. 7. A method contains that takes an xy-rectangle R as the argument and returns true if and only if every point contained in R is also contained in the current xy-rectangle. 8. A method overlapsWith that takes an xy-rectangle R as the argument and returns true if and only if at least one point is contained in both R and this xy-rectangle. Note: 3 You may assume that the reference-typed parameters of the constructor or methods are never null. You may define additional methods when you see fit. Tests in XYRectangle Test.java should all pass after you've completed the class. What to do: In XYRectangle.java [Task 6] Complete the constructor as well as the other methods in class XYRectangle. package hk.edu.polyu.comp.comp2021.assignment1. shape; import org.junit.Test; import org.junit.Before; import static org.junit.Assert.*; public class XYRectangle Test { Point [] [] points; XYRectangle r1, r2, r3, r4, r5, r6; private Point getPoint(int x, int y){ return points [x] [y]; } @Before public void init() { } points = new Point [6] [6]; for(int i = 0; i < 6; i++) @Test for(int j = 0; j < 6; j++) { points [i][j] = new Point (i, j); r1 = new XYRectangle(getPoint(x:1,y:2), getPoint(x:3,y:1)); r2 = new XYRectangle(getPoint(x:1,y:2), getPoint(x: 2,y: 1)); r3 = new XYRectangle(getPoint(x:4,y:4), getPoint(x:5,y:3)); public void testConstructor1() { } assertEquals(" ", r1.toString()); @Test public void testArea() { assertEquals(2, r1.area()); } @Test public void testRotateClockwise1 ( ) {\ r1. rotateClockwise(); assertEquals(" ", r1.toString()); } @Test public void testMovel ( ) { r1.move(1,1); assertEquals(" ", r1.toString()); } @Test public void testContains1() { } assertTrue(r1.contains(getPoint(x: 1,y:2))); @Test public void testContains() { } assertTrue(r1.contains(r2)); @Test public void testOverlapsWith1() { } } assertTrue(r1.overlapsWith(r2)); package hk.edu.polyu.comp.comp2021.assignment1. shape; public class XYRectangle { private Point topleft; private Point bottom Right; public Point getTopLeft() { return topLeft; } public Point getBottom Right() { return bottomRight; } public XYRectangle (Point p1, Point p2) { // Todo: complete the constructor } public String toString() { // Todo: complete the method return ""; } public int area() { // Todo: complete the method return 0; } public void rotateClockwise() { // Todo: complete the method return; } public void move(int deltax, int deltaY) { // Todo: complete the method } public boolean contains (Point p) { // Todo: complete the method return false; } public boolean contains (XYRectangle r) { // Todo: complete the method return false; } public boolean overlapsWith(XYRectangle r) { // Todo: complete the method return false; } class Point{ private int x; private int y; public Point (int x, int y) { set(x, y); } public int getX() { return x; } public int getY() { return y; } public void set (int x, int y) { this.x = x; this.y = y; } } public String toString() { } return "(" + getX() + "," + getY() + ")";