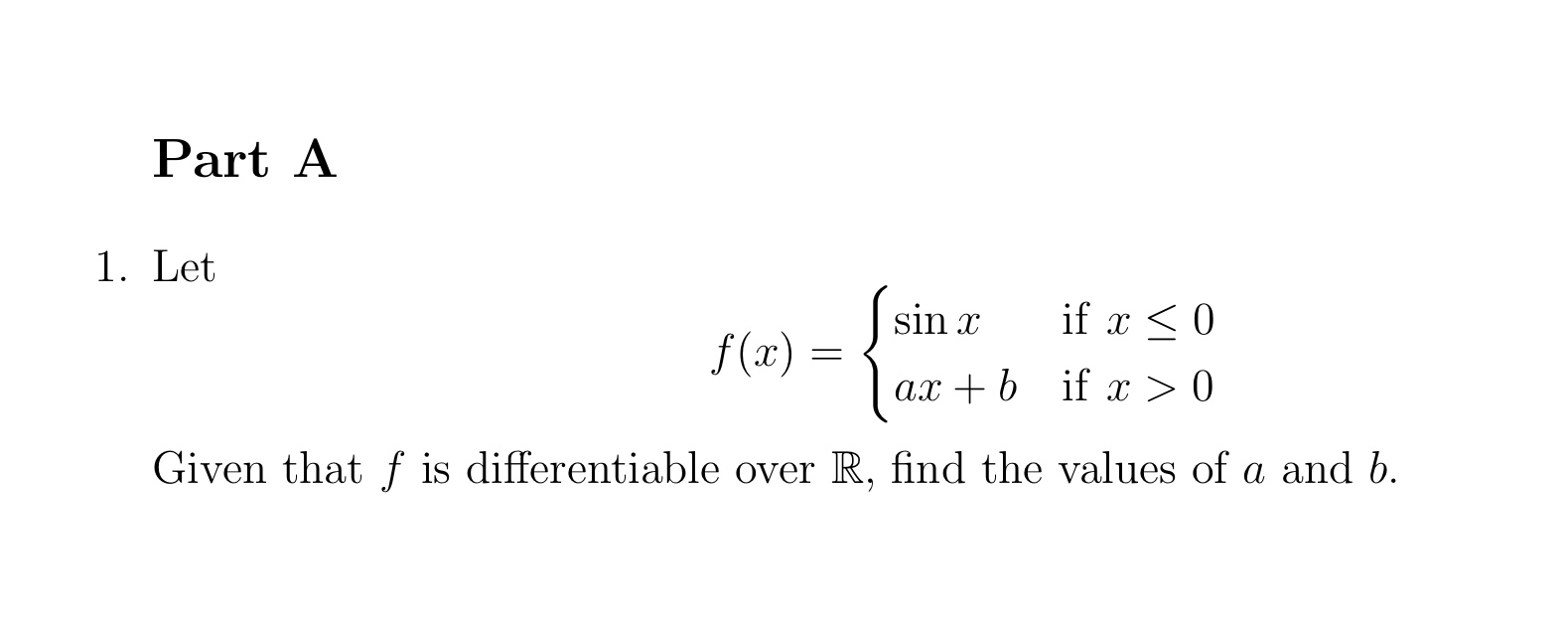
5 7. * Suppose n 3 is a positive integer and f: (0,) (0, ) is an n-times differentiable function such that f(x) f'(x) = 1 for all x (0, ). Given that f(1) = 2, find '(1), (1) and ""(1). 4. This question is to demonstrate that the one-sided derivative L'(a), R'(a) cannot be evaluated by taking one-sided limit of f'(x). Let f(x) = = x sin to 0 (a) Find f'(x) when x 0 (b) Find Rf'(0). (c) Show that Rf'(0) lim f'(x). x 0+ X if x 0, if x = 0. : Part A 1. Let Jsin x (x) = if x < 0 ax + b if x > 0 Given that f is differentiable over R, find the values of a and b. Part B 3. * Suppose that a function f is continuous on the closed interval [0, 1] and that 0 f(x) 1 for every x in [0, 1]. Show that there must exist a number c in [0, 1] such that f(c): = c (c is called a fixed point of ). 5. An ordinary differential equation (ODE) is an equation that relates x, y (func- tion of x) and the derivatives of y. A solution of an ODE is a function y that satisfies such an equation. Consider the following ODE: y is a solution. dt +2k. + ny = 0, dy dt where k, n are constants. Prove that if A, p, c are constants and n then y(t) Ae-kt cos (pt + c) = = p + k, 2. Let u, v be functions of x. The first order derivative of uv can be derived by the following product rule: (uv)' = u'v + uv'. The general n-th order derivative of uv was obtained by the German mathematician Gottfried Wilhelm Leibniz: where (3) k n! k! (n - k)!' By Leibniz's formula, compute f(100) (x) if - Ch n (uv) (") = (1.) u () k k=0 = (k),(n-k) 9 f(x) = (x + 2x + x + 5) cosx.