5 question

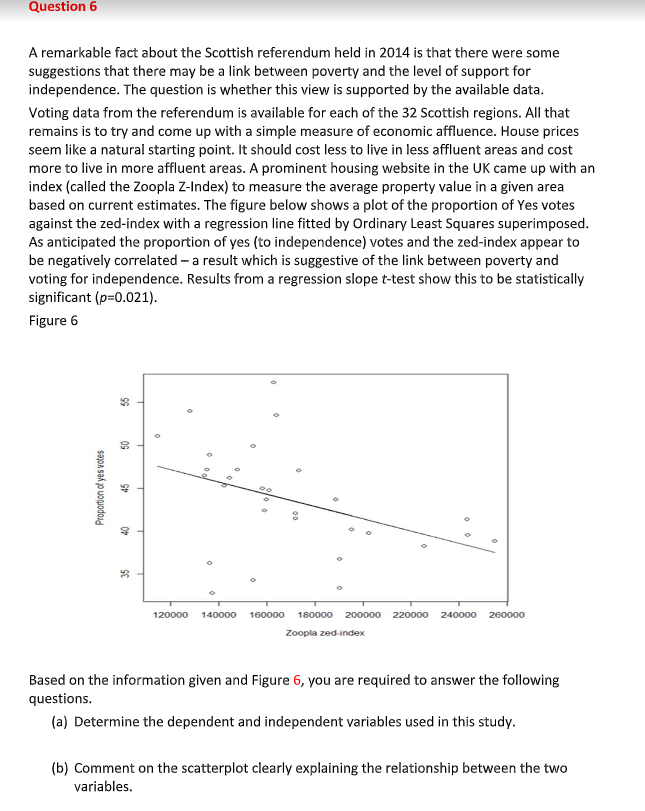
(1) Confidence intervals and tests of significance are two most common types of statistical inference. You are required to explain in a few sentences the fundamental differences between these two types of statistical inference by giving relevant examples when one type of statistical inference method is preferred over the other. (ii) Nutritionists believe that a vegetarian diet has no effect on the height of children. A group of researchers in China studying the effects of diet on growth would like to know if a vegetarian diet affects the height of a child. The researchers randomly selected 300 vegetarian children in China who are five years old. The average height of these children was found to be 44.5 inches with a standard deviation of 3.8 inches. The average height for all five-year-old children in China is known to be 45.75 inches. Conduct a hypothesis test to determine whether there is overwhelming evidence at a=.05 that five-year-old vegetarian children are not the same height as other five-year-old children in China. Assume that the height of a five-year-old vegetarian child in China is approximately normally distributed.Question 3 In a study on "Attitudes to Social Spending in Newfoundland", a sample of 91 adults in Eastern and Central Newfoundland was taken in early 1988 to examine public attitudes toward government cuts in social spending. Some of the results from this study are described in Morris Saldov's paper titled "Public Attitudes to Social Spending in Newfoundland," Canadian Review of Social Policy, 26, November 1990. Based on the data for this study as shown in Table 3.1, the author comments that respondents who knew someone on social assistance, were more likely to feel that welfare spending were too low. Table 3.1 View on Welfare Spending \\ Knows Someone on Social Assistance Yes No Total Too Little 40 6 46 About Right 16 13 29 Too Much 9 7 16 Total 65 26 91 a) Calculate the relevant conditional probabilities using the author's concerns on whether knowing someone on social assistance may influence their view on welfare spending. What do these results show? b) Calculate the expected frequencies for the above cross- tabulation assuming that knowing someone on social assistance and their view on welfare spending are independent of one another. c) Are the expected frequencies calculated above consistent with the requirements for a valid Chi-Square test? d) Is there sufficient evidence to indicate a significant association between knowing someone on social assistance and their view on welfare spending at the 5% significance level?(cl Write down a regression model depicting the relationship between the two variables. Please ensure you explain each symbol used In the model and equation. Question 6 A remarkable fact about the Scottish referendum held in 2014 is that there were some suggestions that there may be a link between poverty and the level of support for independence. The question is whether this view is supported by the available data. Voting data from the referendum is available for each of the 32 Scottish regions. All that remains is to try and come up with a simple measure of economic affluente. House prices seem like a natural starting point. It should cost less to live in less affluent areas and cost more to live in more affluent areas. A prominent housing website in the UK came up with an index (called the Zoopla Z-Index) to measure the average property value in a given area based on current estimates. The figure below shows a plot of the proportion of Yes votes against the zed-index with a regression line fitted by Ordinary Least Squares superimposed. As anticipated the proportion of yes (to independence) votes and the zed-index appear to be negatively correlated - a result which is suggestive of the link between poverty and voting for independence. Results from a regression slope t-test show this to be statistically significant (p=0.021). Figure 6 Proportion of yes votes 120000 140000 160000 180000 200000 220000 240000 260000 Zoopla zed index Based on the information given and Figure 6, you are required to answer the following questions. (a) Determine the dependent and independent variables used in this study. (b) Comment on the scatterplot clearly explaining the relationship between the two variables.Question 7 A marketing manager of a leading firm believes that total sales for the firm next year can be modelled by using a normal distribution, with a mean of AUD$2.5 million and a standard deviation of AUD$300,000. a) What is the probability that the firm's sales will exceed AUD$3 million? b) In order to cover fixed costs, the firm's sales must exceed the break-even level of AUD$1.8 million. What is the probability that sales will exceed the break-even level? c) Determine the sales level that has only a 9% chance of being exceeded next year