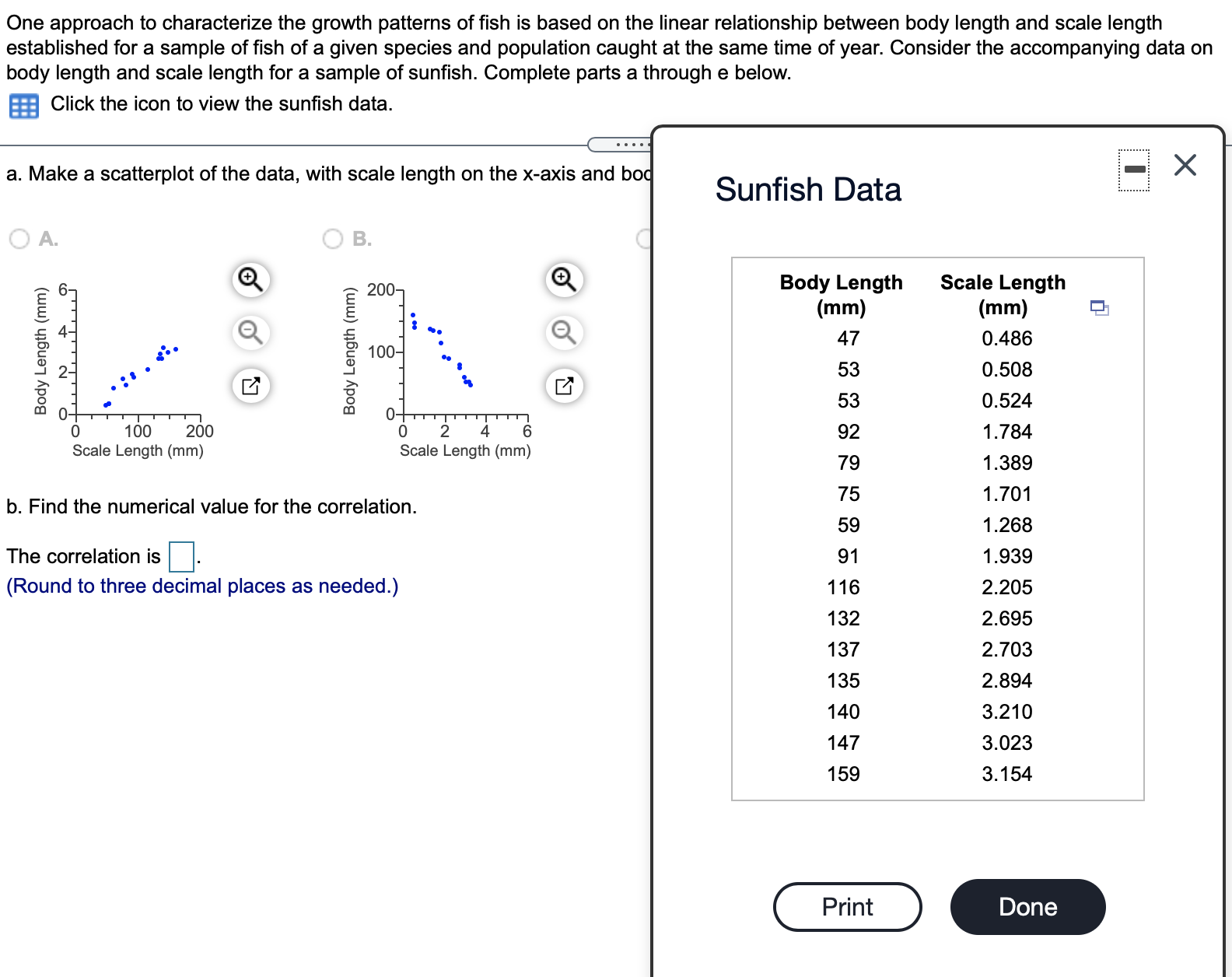
5 STAT QUESTIONS

1. 

The scatterplot shows the median annual pay, in dollars per year, for men and women in various cities. The correlation is 0.90. The regression equation is shown below. Complete parts a and b below. Predicted Women = 8795 + 0.5908 Men Women's Median Pay 40000 60000 80000 Men's Median Pay .1: a. Find a rough estimate (by using the scatterplot) of median pay for women in a city that has a median pay of about $50,000 for men. A. Between $25,000 and $35,000 3 B. Between $35,000 and $45,000 C. Between $55,000 and $65,000 D. Between $45,000 and $55,000 b. Use the given regression equation to get a more precise estimate of the median pay for women in a city that has a median pay for men of $50,000. The estimated median pay for women is $D. Assume that in a political science class, the teacher gives a midterm exam and a final exam. Assume that the association between midterm and final scores is linear. The summary statistics shown below have been simplified for clarity. Also, r = 0.7 and n = 30. Mean Standard deviation Midterm 72 10 Final 72 10 According to the regression equation, for a student who gets a 95 on the midterm, what is the predicted final exam grade? What phenomenon does this demonstrate? Explain. . . . . . The predicted final exam grade is (Round to the nearest integer as needed.)One approach to characterize the growth patterns of fish is based on the linear relationship between body length and scale length established for a sample of fish of a given species and population caught at the same time of year. Consider the accompanying data on body length and scale length for a sample of sunfish. Complete parts a through e below. Click the icon to view the sunfish data. a. Make a scatterplot of the data, with scale length on the x-axis and bod X Sunfish Data O A. O B. Lg 200- Body Length Scale Length (mm) (mm) 47 0.486 Body Length (mm) Body Length (mm) 100- N 53 . . 0.508 53 0.524 100 200 0 2 4 92 1.784 Scale Length (mm) Scale Length (mm) 79 1.389 75 1.701 b. Find the numerical value for the correlation. 59 1.268 The correlation is. 91 1.939 (Round to three decimal places as needed.) 116 2.205 132 2.695 137 2.703 135 2.894 140 3.210 147 3.023 159 3.154 Print Done