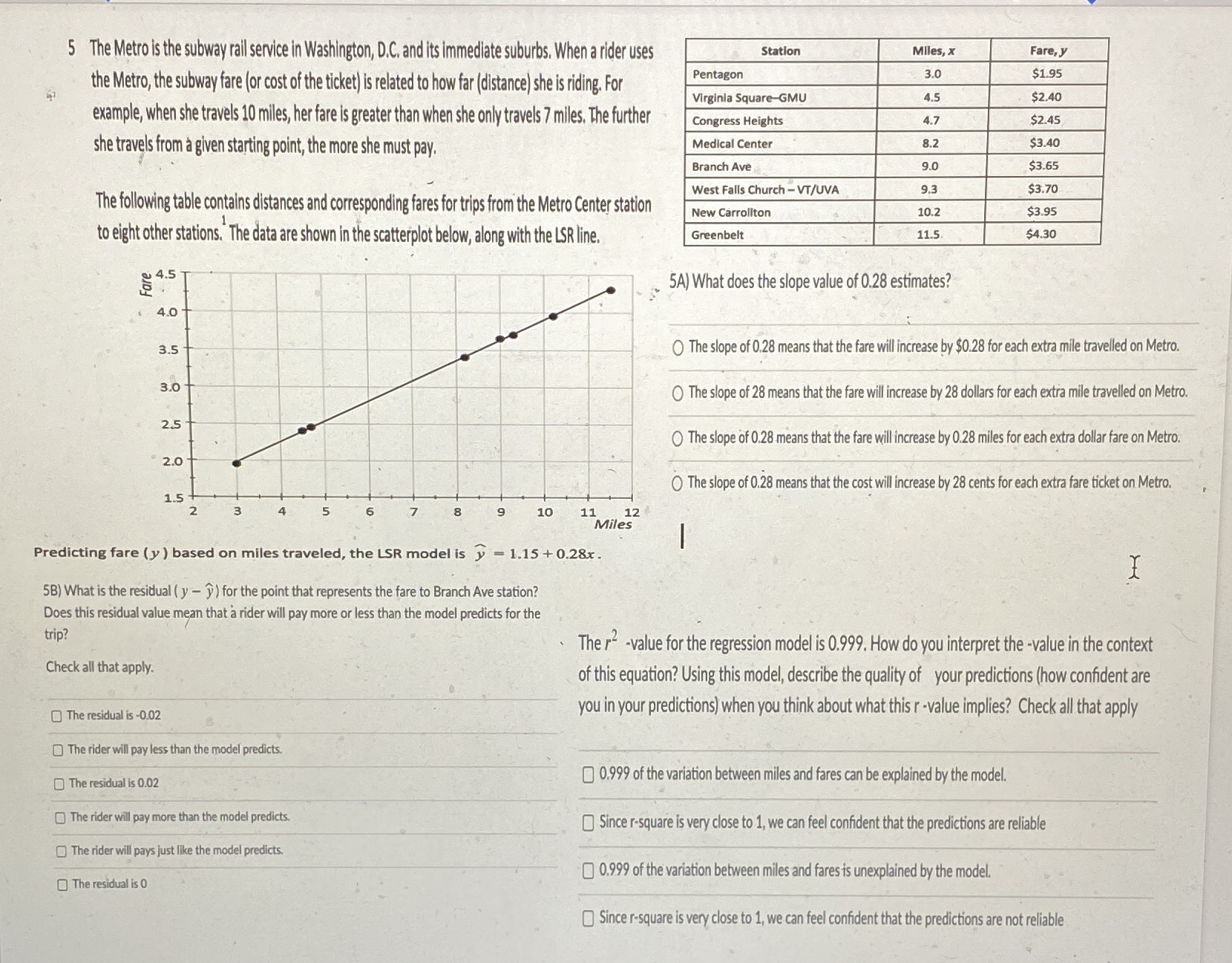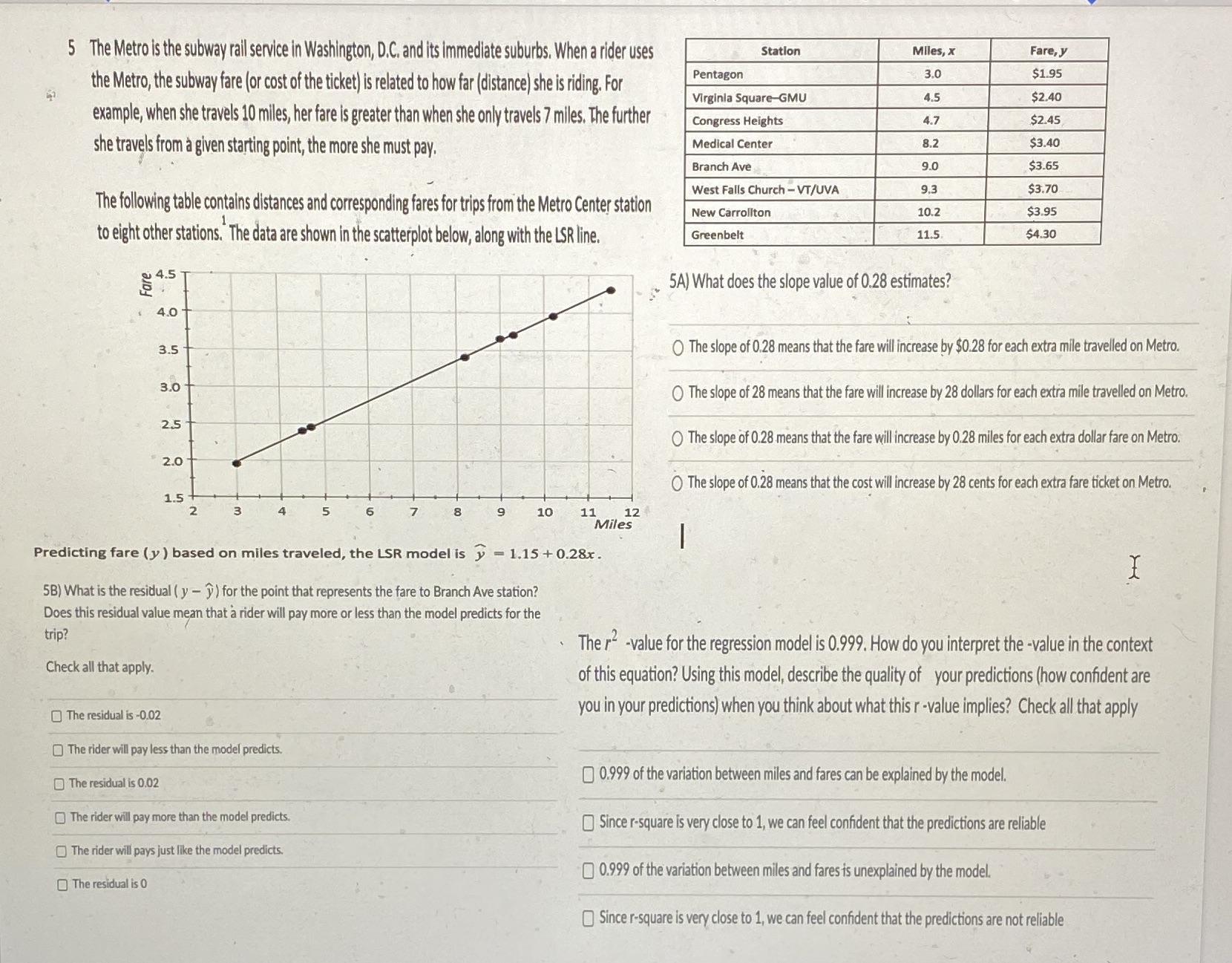
5 The Metro is the subway rail service in Washington, D.C. and its immediate suburbs. When a rider uses Station Miles, x Fare, J the Metro, the subway fare (or cost of the ticket) is related to how far (distance) she is riding. For Pentagon 3.0 $1.95 Virginia Square-GMU 4.5 $2.40 example, when she travels 10 miles, her fare is greater than when she only travels 7 miles. The further Congress Heights 4.7 $2.45 she travels from a given starting point, the more she must pay. Medical Center 8.2 $3.40 Branch Ave 9.0 $3.65 West Falls Church - VT/UVA 9 .3 $3.70 The following table contains distances and corresponding fares for trips from the Metro Center station New Carrollton 10.2 $3.95 to eight other stations. "The data are shown in the scatterplot below, along with the LSR line. Greenbelt 11.5 $4.30 @ 4.5 5A) What does the slope value of 0.28 estimates? 4.0 35 The slope of 0.28 means that the fare will increase by $0.28 for each extra mile travelled on Metro. 3.0 The slope of 28 means that the fare will increase by 28 dollars for each extra mile travelled on Metro. 2.5 The slope of 0.28 means that the fare will increase by 0.28 miles for each extra dollar fare on Metro. 20 The slope of 0.28 means that the cost will increase by 28 cents for each extra fare ticket on Metro. 1.5 10 11 12 Miles Predicting fare (y ) based on miles traveled, the LSR model is y = 1.15 +0.28x. 5B) What is the residual ( y - y ) for the point that represents the fare to Branch Ave station? Does this residual value mean that a rider will pay more or less than the model predicts for the trip? The r -value for the regression model is 0.999. How do you interpret the -value in the context Check all that apply. of this equation? Using this model, describe the quality of your predictions (how confident are The residual is -0.02 you in your predictions) when you think about what this r-value implies? Check all that apply O) The rider will pay less than the model predicts. The residual is 0.02 [) 0.999 of the variation between miles and fares can be explained by the model. ) The rider will pay more than the model predicts. Since r-square is very close to 1, we can feel confident that the predictions are reliable The rider will pays just like the model predicts. 0.999 of the variation between miles and fares is unexplained by the model. The residual is O Since r-square is very close to 1, we can feel confident that the predictions are not reliable