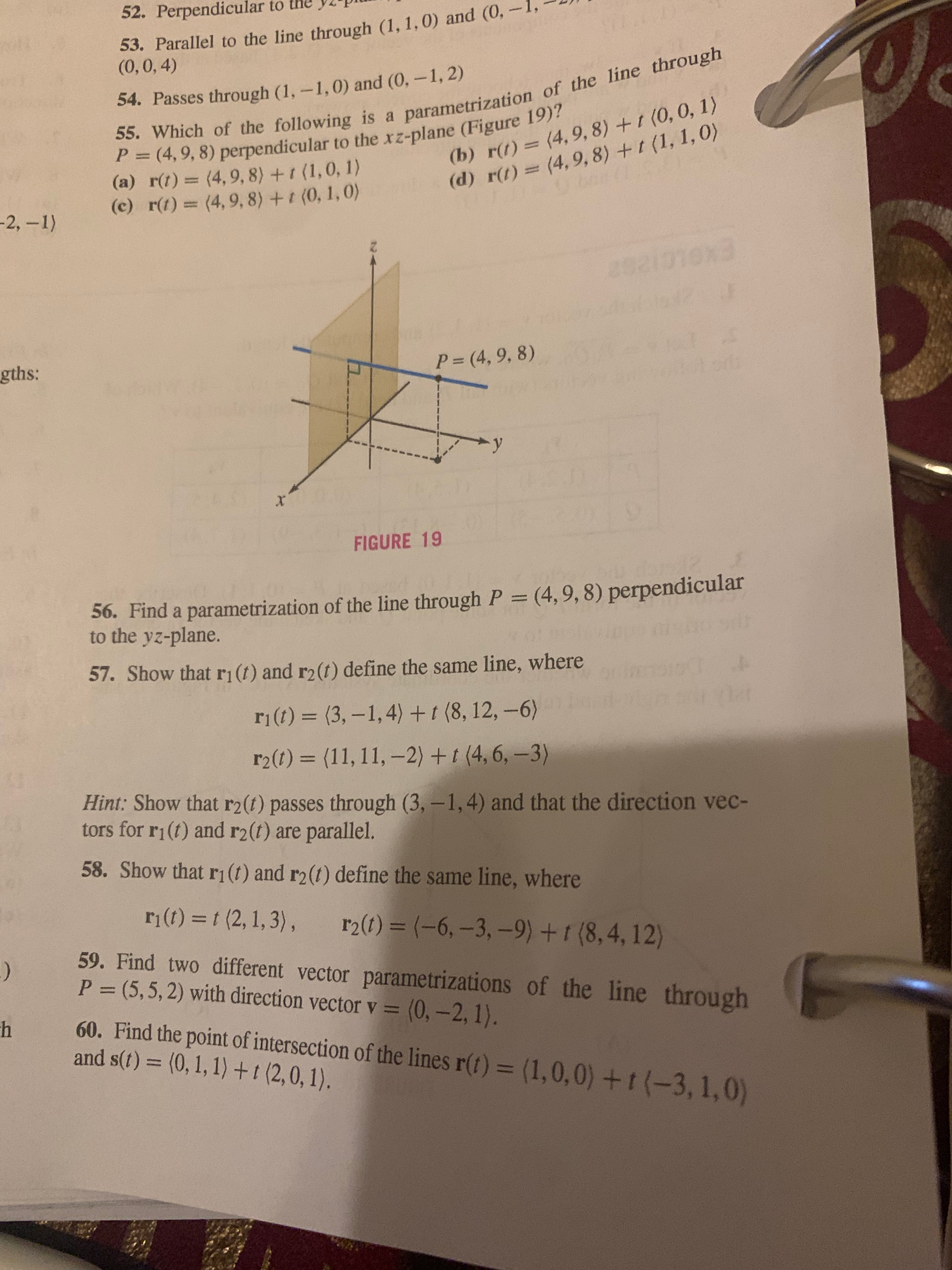
52. Perpendicular to the 53. Parallel to the line through (1, 1, 0) and (0, -1, (0, 0, 4) 54. Passes through (1, -1, 0) and (0, -1, 2) 55. Which of the following is a parametrization of the line through P = (4, 9, 8) perpendicular to the xz-plane (Figure 19)? (b) r(t) = (4, 9, 8) + t (0, 0, 1) (a) r(t) = (4, 9, 8) + 1 (1, 0, 1) (d) r(t) = (4, 9, 8) + 1 (1, 1, 0) (c) r(t) = (4, 9, 8) + 1 (0, 1, 0) -2, - 1) gths: P = (4, 9, 8) FIGURE 19 56. Find a parametrization of the line through P = (4, 9, 8) perpendicular to the yz-plane. 57. Show that ri(t) and r2(t) define the same line, where ri (t) = (3, -1, 4) +t(8, 12, -6) r2(t) = (11, 11, -2) + t (4, 6, -3) Hint: Show that r2(t) passes through (3, -1, 4) and that the direction vec- tors for ri(t) and r2(t) are parallel. 58. Show that ri(t) and r2(t) define the same line, where ri(t) = t (2, 1, 3), 12 (1 ) = (-6, -3, -9) + 1(8, 4, 12) 59. Find two different vector parametrizations of the line through P = (5, 5, 2) with direction vector v = (0, -2, 1). 60. Find the point of intersection of the lines r(t) = (1, 0,0) + t (-3, 1, 0) and s(t) = (0, 1, 1) + t (2, 0, 1).SECTION 13.2 Thre 61. Show that the lines ri(t) = (-1, 2, 2) + t (4, -2, 1) and rz(t) = 70. Find the co midpoint of AB (0, 1, 1) + t (2, 0, 1) do not intersect. 62. Determine whether the lines ri (t) = (2, 1, 1) + t (-4, 0, 1) and 12(s) = (-4, 1,5) + s (2, 1, -2) intersect, and if so, find the point of in-orange tersection. nod potwol 63. Determine whether the lines ri(t) = (0, 1, 1) + t (1, 1, 2) and r2(s)= (2, 0, 3) + s (1, 4, 4) intersect, and if so, find the point of intersection,A 64. Find the intersection of the lines ri(t) = (-1, 1) + t (2, 4) and r2(s)as (2, 1) + s (-1, 6) in the plane. 65. A meteor follows a trajectory r(t) = (2, 1, 4) + t (3, 2, -1) km with in minutes, near the surface of the earth, which is represented by the xy- plane. Determine at what time the meteor hits the ground. 66. A laser's beam shines along the ray given by ri(t) = (1, 2, 4) + t(2, 1, -1) for t 2 0. A second laser's beam shines along the ray given by r2(s) = (6, 3, -1) + s(-5,2, c) for s 2 0, where the value of c allows for the adjustment of the z-coordinate of its direction vector. Find the value 71. A box of c that will make the two beams intersect. crane has a cables, each 67. The line with vector parametrization r(t) = (3, 1, -4) + t (-2, -2, 3) below the 1 intersects the sphere (x - 1) + (y + 3)+ z2 = 8 in two points. Find on each cal them. Hint: Determine t such that the point (x(t), y(t), z(t)) satisfies the equation of the sphere, and then find the corresponding points on the line. 68. Show that the line with vector parametrization r(t) = (3, 5, 6) + t (1, -2, -1) does not intersect the sphere of radius 5 centered at the origin. 69. Find the components of the vector v whose tail and head are the mid- points of segments AC and BC in Figure 20. [Note that the midpoint of (a1, a2, a3) and (b1, b2, b3) is a1 + bi a2 + 62 a3 + b3 2 2 2 Further Insights and Challe