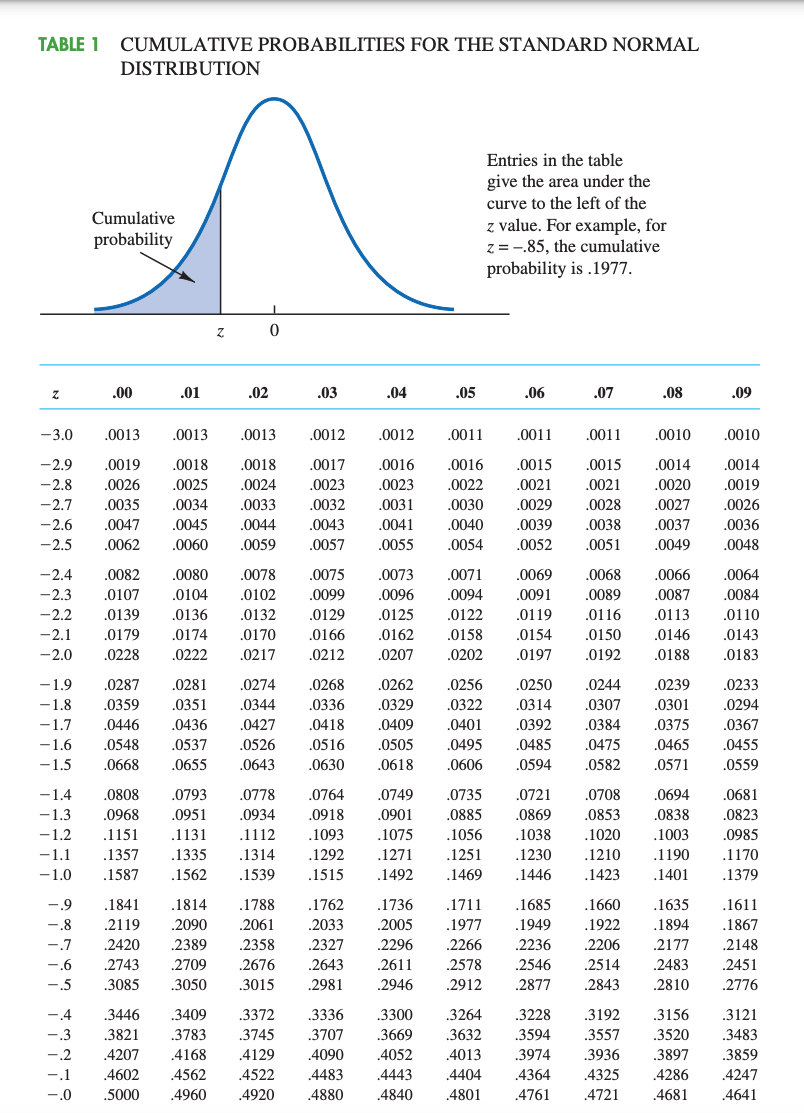
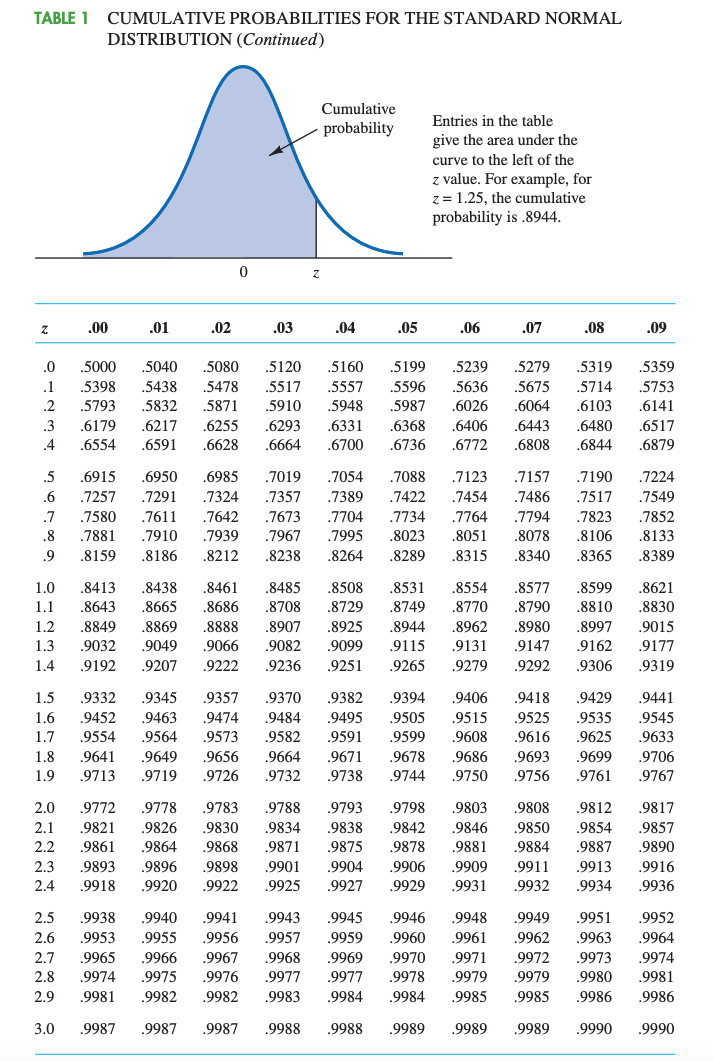
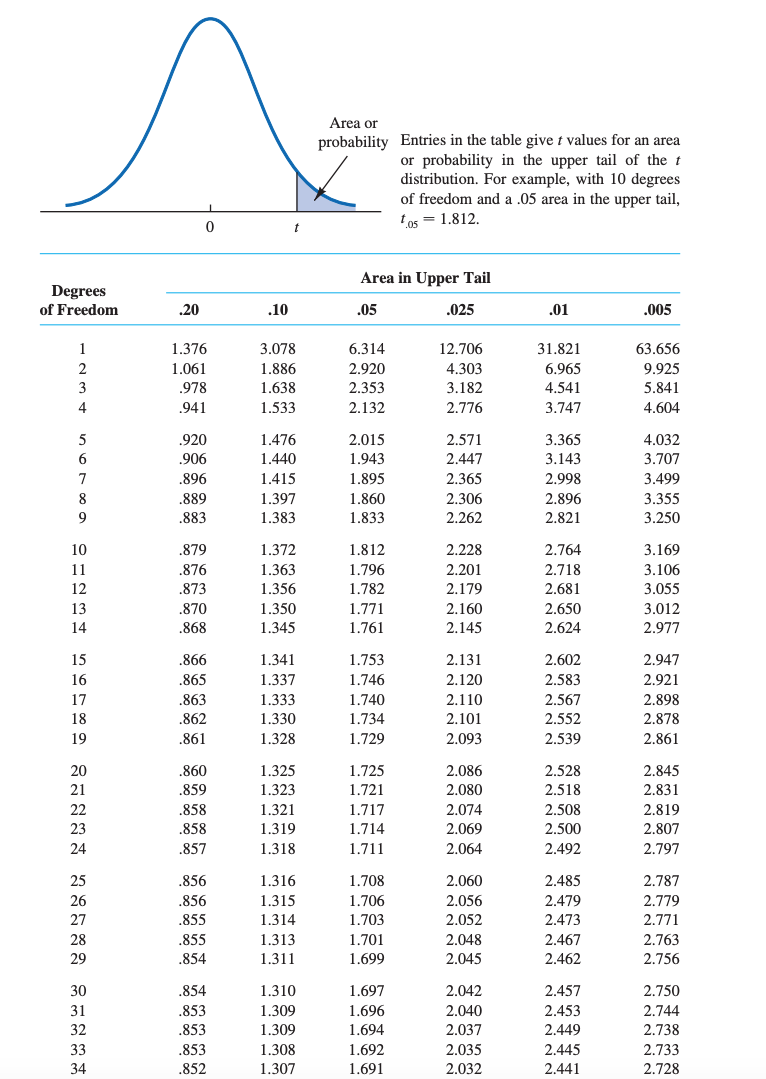
7. [-/4.54 Points] DETAILS ASWSBE14 6.E.015. You may need to use the appropriate appendix table to answer this question. Given that z is a standard normal random variable, find z for each situation. (Round your answers to two decimal places.) (a) The area to the left of z is 0.2119. (b) The area between -z and z is 0.9232. (c) The area between -z and z is 0.2282. (d) The area to the left of z is 0.9949. (e) The area to the right of z is 0.5793.8. [-I4,54 Points] ASWSBE14 6.E.017. ASK YOUR TEACHER PRACTICE ANOTHER Males in the Netherlands are the tallest, on average, in the world with an average height of 183 centimeters (cm).i Assume that the height of men in the Netherlands is normally distributed with a mean of 183 cm and standard deviation of 10.5 cm. You may need to use the appropriate appendix table to answer this question. (a) What is the probability that a Dutch male is shorter than 176 cm? (Round your answer to four decimal places.) H (b) What is the probability that a Dutch male is taller than 194 cm? (Round your answer to four decimal places.) H (c) What is the probability that a Dutch male is between 174 and 192 cm? (Round your answer to four decimal places.) H (d) Out of a random sample of 1,000 Dutch men, how many would we expect to be taller than 189 cm? (Round your answer to the nearest integer.) H men TABLE I CUMULATIVE PROBABILITIES FOR THE STANDARD NORMAL DISTRIBUTION Entries in the table give the area under the curve to the left of the z value. Fer example, for z = .85, the cumulative probability is .1977. Cumulative probability 2. .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 3.0 .0013 .0013 .0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 -2.9 .0019 .0018 .0018 .0017 .0016 .0016 .0015 .0015 .0014 .0014 2.8 .0026 .0025 .0024 .0023 .0023 .0022 .0021 .0021 .0020 .0019 - 2.7 .0035 .0034 .0033 .003 2 .0031 .0030 .0029 .0028 .0027 .0026 -2.6 .0047 .0045 .0044 .0043 .0041 .0040 .0039 .0038 .0037 .0036 2.5 .0062 .0060 .0059 .0057 .0055 .0054 .0052 .0051 .0049 .0048 -2.4 .0082 .0080 .007 8 .0075 .007 3 .0071 .0069 .0068 .0066 .0064 2.3 .0107 .0104 .0102 .0099 .0096 .0094 .0091 .0089 .0087 .0084 2.2 .0139 .0136 .0132 .0129 .0125 .0122 .0119 .0116 .0113 .0110 -2.1 .0179 .0174 .0170 .0166 .0162 .0158 .0154 .0150 .0146 .0143 2.0 .0228 .0222 .0217 .0212 .0207 .0202 .0197 .0192 .0188 .0183 1.9 .0287 .0281 .0274 .0268 .0262 .0256 .0250 .0244 .0239 .0233 1.8 .0359 .0351 .0344 .0336 .0329 .0322 .0314 .0307 .0301 .0294 1.7 .0446 .0436 .0427 .0418 .0409 .0401 .0392 .0384 .0375 .0367 1.6 .0548 .0537 .0526 .0516 .0505 .0495 .0485 .0475 .0465 .0455 1.5 .0668 .0655 .0643 .0630 .0618 .0606 .0594 .0582 .0571 .0559 1.4 .0808 .0793 .0778 .0764 .0749 .0735 .0721 .0708 .0694 .0681 - 1.3 .0968 .0951 .0934 .0918 .0901 .0885 .0869 .0853 .0838 .0823 1.2 .1151 .1131 .1112 .1093 .1075 .1056 .1038 .1020 .1003 .0985 1.1 .1357 .1335 .1314 .1292 .1271 .1251 .1230 .1210 .1190 .1170 -1.0 .1587 .1562 .1539 .1515 .1492 .1469 .1446 .1423 .1401 .1379 .9 .1841 .1814 .1788 .1762 .1736 .1711 .1685 .1660 .1635 .1611 .8 .2119 .2090 .2061 .2033 .2005 .1977 .1949 .1922 .1894 .1867 .7 .2420 .2389 .2358 .2327 .2296 .2266 .2236 .2206 .2177 .2148 .6 .2743 .2709 .2676 .2643 .261 1 .2578 .2546 .2514 .2483 .2451 .5 .3085 .3050 .3015 .2981 .2946 .2912 .2877 .2843 .2810 .2776 .4 .3446 .3409 .3372 .3336 .3300 .3264 .3228 .3192 .3156 .3121 .3 .3821 .3783 .3745 .3707 .3669 .3632 .3594 .3557 .3520 .3483 -.2 .4207 .4168 .4129 .4090 .4052 .4013 .3974 .3936 .3897 .3859 .1 .4602 .45 62 .4522 .4483 .4443 .4404 .4364 .4325 .4286 .4247 .0 .5000 .4960 .4920 .4880 .4840 .4801 .4761 .4721 .4681 .4641 TABLE 1 CUMULATIVE PROBABILITIES FOR THE STANDARD NORMAL DISTRIBUTION (Continued) Cumulative probability Entries in the table give the area under the curve to the left of the z value. For example, for z = 1.25, the cumulative probability is .8944. 0 Z 2 .00 .01 .02 .03 .04 .05 .06 .07 .08 09 .5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359 .5398 .5438 5478 5517 .5557 .5596 .5636 .5675 5714 .5753 .5793 .5832 .5871 .5910 .5948 5987 .6026 .6064 6103 6141 .6179 6217 .6255 .6293 .6331 .6368 .6406 .6443 6480 6517 4 .6554 .6591 .6628 .6664 6700 6736 .6772 .6808 6844 6879 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 7224 bau .7257 .7291 .7324 .7357 7389 7422 .7454 .7486 .7517 7549 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 .7881 .7910 .7939 .7967 7995 .8023 .8051 .8078 .8106 8133 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 8365 .8389 1.0 .8413 .8438 .8461 8485 8508 8531 .8554 .8577 .8599 8621 1.1 .8643 .8665 .8686 .8708 8729 8749 .8770 .8790 8810 .8830 1.2 .8849 .8869 .8888 .8907 .8925 .8944 .8962 .8980 8997 .9015 1.3 .9032 .9049 .9066 .9082 .9099 9115 .9131 .9147 .9162 .9177 1.4 .9192 .9207 .9222 .9236 .9251 .9265 .9279 .9292 .9306 .9319 1.5 .9332 .9345 .9357 .9370 .9382 .9394 .9406 .9418 .9429 .9441 1.6 .9452 .9463 .9474 .9484 9495 .9505 .9515 .9525 .9535 9545 1.7 .9554 .9564 .9573 .9582 .9591 .9599 .9608 .9616 .9625 .9633 1.8 .9641 .9649 .9656 .9664 .9671 .9678 .9686 .9693 .9699 9706 1.9 .9713 .9719 .9726 .9732 .9738 9744 9750 .9756 9761 .9767 2.0 .9772 .9778 .9783 .9788 9793 .9798 .9803 .9808 .9812 .9817 2.1 .9821 .9826 .9830 .9834 .9838 .9842 .9846 .9850 9854 9857 2.2 .9861 .9864 .9868 .9871 .9875 9878 .9881 .9884 9887 9890 2.3 .9893 .9896 .9898 .9901 .9904 .9906 .9909 .9911 9913 .9916 2.4 .9918 .9920 .9922 .9925 .9927 .9929 .9931 .9932 .9934 9936 2.5 .9938 .9940 .9941 .9943 9945 .9946 .9948 .9949 9951 9952 2.6 .9953 9955 .9956 .9957 9959 .9960 .9961 .9962 .9963 9964 2.7 .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974 2.8 .9974 9975 9976 9977 9977 9978 .9979 .9979 .9980 9981 2.9 .9981 .9982 .9982 9983 9984 .9984 .9985 .9985 .9986 .9986 3.0 .9987 .9987 .9987 .9988 .9988 .9989 .9989 .9989 .9990 .9990Area or probability Entries in the table give I values for an area or probability in the upper tail of the 1 distribution. For example, with 10 degrees of freedom and a .05 area in the upper tail, 0 t {05 = 1.3 12. Area in Upper Tail Degrees of Freedom .20 .10 .05 .025 .01 .005 1 1.376 3.073 6.314 12.706 31.321 63.656 2 1.061 1.336 2.920 4.303 6. 965 9.925 3 .973 1.633 2.353 3.132 4.541 5.341 4 .941 1.533 2.132 2.776 3.747 4.604 5 .920 1.476 2.015 2.571 3. 365 4.032 6 .906 1.440 1.943 2.447 3.143 3.707 7 .396 1.415 1.395 2.365 2. 993 3.499 3 .339 1.397 1.360 2.306 2. 396 3.355 9 .333 1.333 1.333 2.262 2.321 3.250 10 .379 1.372 1.312 2.223 2.764 3.169 1 1 .376 1.363 1.796 2.201 2.713 3.106 12 .373 1.356 1.732 2.179 2.631 3.055 13 .370 1.350 1.771 2.160 2.650 3.012 14 .363 1.345 1.761 2.145 2.624 2.977 15 .366 1.341 1.753 2.131 2.602 2.947 16 .365 1.337 1.746 2.120 2.533 2.921 17 .363 1.333 1.740 2.110 2.567 2.393 13 .362 1.330 1.734 2.101 2.552 2.373 19 .361 1.323 1.729 2.093 2.5 39 2.361 20 .360 1.325 1.725 2.036 2.523 2.345 21 .359 1.323 1.721 2.030 2.513 2.331 22 .353 1.321 1.717 2.074 2.503 2.319 23 .353 1.319 1.714 2.069 2.500 2.307 24 .357 1.313 1.71 1 2.064 2.492 2.797 25 .35 6 1.316 1.703 2.060 2.435 2.737 26 .35 6 1.315 1.706 2.05 6 2.479 2.779 27 .355 1.314 1.703 2.052 2.473 2.771 23 .35 5 1.313 1.701 2.043 2.467 2.763 29 .354 1.311 1.699 2.045 2.462 2.756 3 0 .354 1.310 1.697 2.042 2.457 2.750 31 .35 3 1.309 1.696 2.040 2.453 2.744 3 2 .35 3 1.309 1.694 2.037 2.449 2.733 3 3 .35 3 1.303 1.692 2.035 2.445 2.733 34 .352 1.307 1.691 2.032 2.441 2.723