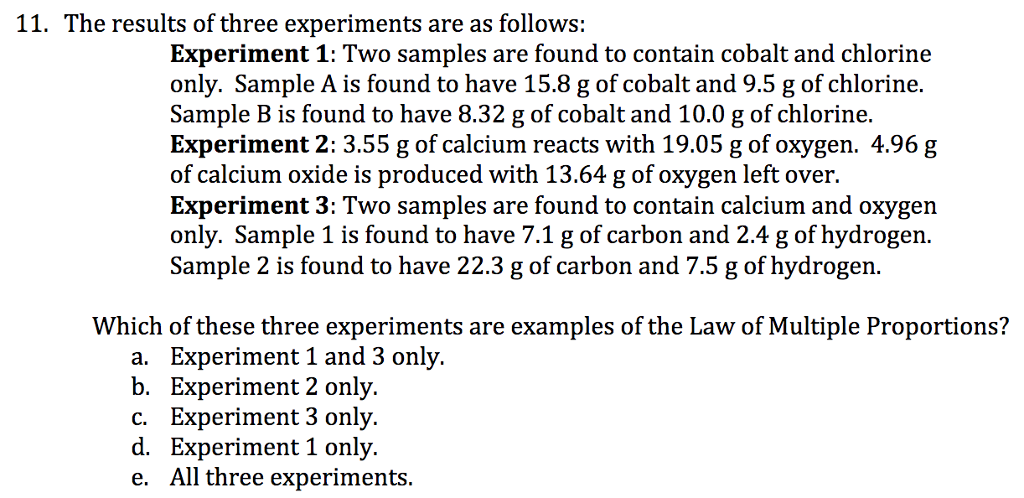73% of understudies like in-class figuring out how to internet learning. Assume we arbitrarily select 100 undergrads and get some information about their in-class versus online inclination. Leave X alone the quantity of these understudies who like in-class learning. Let p = the likelihood of a specific single understudy liking in-class learning.

a. What is the likelihood that X is inside 2.0 standard deviations of its normal worth?

b. What is the generally anticipated worth of 0.73X?

c. What is the standard deviation of X - 5 ?

d. What is the change of 0.73X?

Philippine General Hospital (PGH) agony about line in trauma centers. The clinical staff close by can't oblige the patient on-line if there are in excess of 10 crisis cases in a given hour. It is accepted that patient appearance follows a Poisson interaction, and verifiable information recommend that, all things considered, 8 crises show up each hour. What is the likelihood that in excess of 25 crises show up during a 2-hour shift?"

m2m

Bert has a record of shutting on the primary call 70% of the time, with the likelihood of a deal dropping 10% with each progressive call. Riley has a record of shutting on the principal call 56% of the time, with the likelihood of a deal dropping 5% with each progressive call. On the off chance that Bert and Riley make their deal on the fourth call to some random customer (which is depedent on earlier occasions), what is the likelihood of a deal? In light of their outcomes, whom should the board give up and whom would it be a good idea for them to keep?

Information from Excel

first P

second P

third P

fourth P

P

Bert

0.7

0.6

0.5

0.4

0.3

Riley

0.56

0.51

0.46

0.41

0.36

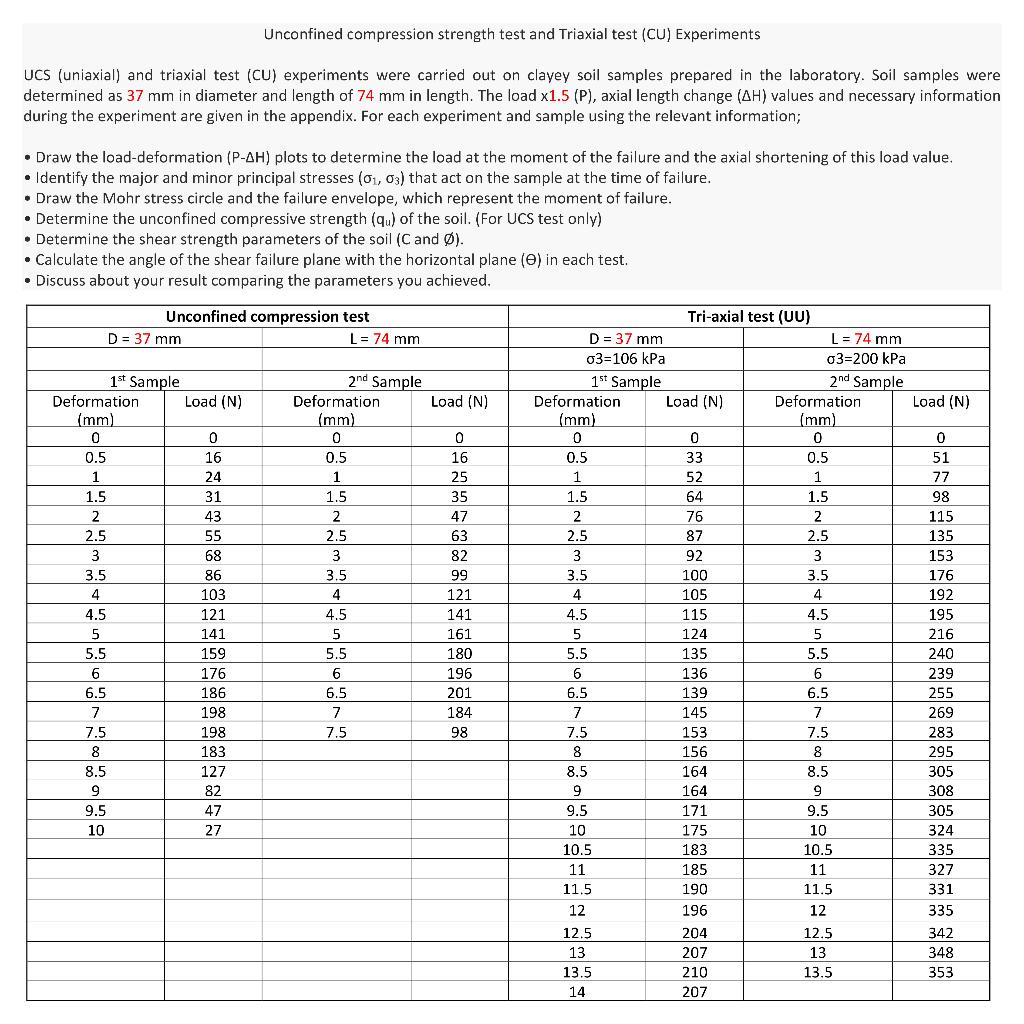
A potential review of diagram besting vehicle on the planet is currently a significant worry of its producer. The issues of this vehicle are from deserts on its frameworks; 0.20 disappointment is plausible from the stopping mechanism, a likelihood of 0.30 from

Suppose that today one share of Microsoft is worth 30 dollars. Suppose that each day, with probability .1 the stock goes up one dollar, and with probability,r .9 the stock goes down one dollar, independent of how it has moved on all other days, Consider the following experiment and sample space. Experiment E: Record the value of Microsoft's stock one day from now, two days from now, three days from now, and four days from now. Sample space S: {i 1, 1, 1, 1M 1, 1, 1,:1),( 1, 1,:1, 1M 1, 1,:1,+1), (1, +1, 1, 1},(1, +1, 1, +1], [1, +1, +1, 1),{1, +1, +1, +1), (+1, 1, 1, 1),[+1,1, 1, +1), (+1, 1, +1, 1),{+1,1, +1, +1), (+1,+1. 1. 1), (+1.+1, 1,+1), (+1. +1.+1, 1), (+1, +1,+1, +11}, with the rst component describing the value of the stock one day from now minus the value of the stock today, the second component describing the value of the stock two days from now minus the value of the stock one day from now, the third component describing the value of the stock three days from now minus the value of the stock two days from now, and the fourth component describing the value of the stock four days from now minus the value of the stock three days from HOW. Consider the event A on sample space S: - As an English Question: I\"illu'ill it be true that the value of the stock at the end of the four days equals either 34 or 26'?" a [2 points) : Express A as a set of outcomes, explicitly listing all outcomes belonging to the event, b (2 points) : Compute P{A) Unconfined compression strength test and Triaxial test {CU} Experiments UCS {uniaxiaIJ and triaxial test {CU} experiments were carried out on clavey soil samples prepared in the laboratory. Soil samples were determined as 37 mm in diameter and length of 74 mm in length. The load x1.5 [P], axial length change {H} values and necessary,r information during the experiment are given in the appendix. For each experiment and sample using the relevant information; - Draw the loaddeformation {PoH] plots to determine the load at the moment of the failure and the axial shortening of this load value. 0 Identify the major and minor principal stresses (0;, 03} that act on the sample at the time of failure. - Draw the Mohr stress circle and the failure envelope, which represent the moment of failure. 0 Determine the unconfined compressive strength [Clul ofthe soil. {For UCS test only] - Determine the shear strength parameters of the soil [C and (2)}. 0 Calculate the angle of the shear failure plane with the horizontal plane {GI} in each test. - Discuss about your result comparing the parameters you achieved. Unconfined compression test Triaxial test {UU} D=37mm L=74 mm D=37mm L=74mm 03:105 kPa 03:200 kPa 2"\" Sample 1\" Sam 2"d Sample Deformation imml Deformation l'mm} Load [N] Deformation imml le T Load [N] Deformation immi Load (N) U [i [I 0 D 0 0 0.5 1 0.5 1 15 25 0.5 1 33 52 0.5 1 51 77 1.5 1.5 35 1.5 64 1.5 98 2 2 47 2 75 2 115 2.5 2.5 53 2.5 87 2.5 135 3. 3.5 3 3.5 .32.. 99 3. 3.5 92 3 3.5 153 176 4 4 4 4 192 195 216 210 353 207 11. The results of three experiments are as follows: Experiment 1: Two samples are found to contain cobalt and chlorine only. Sample A is found to have 15.8 g of cobalt and 9.5 g of chlorine. Sample B is found to have 8.32 g of cobalt and 10.0 g of chlorine. Experiment 2: 3.55 g of calcium reacts with 19.05 g of oxygen. 4.96 g of calcium oxide is produced with 13.64 g of oxygen left over. Experiment 3: Two samples are found to contain calcium and oxygen only. Sample 1 is found to have 7.1 g of carbon and 2.4 g of hydrogen. Sample 2 is found to have 22.3 g of carbon and 7.5 g of hydrogen. Which of these three experiments are examples of the Law of Multiple Proportions? a. Experiment 1 and 3 only. b. Experiment 2 only. c. Experiment 3 only. (1. Experiment 1 only. e. All three experiments