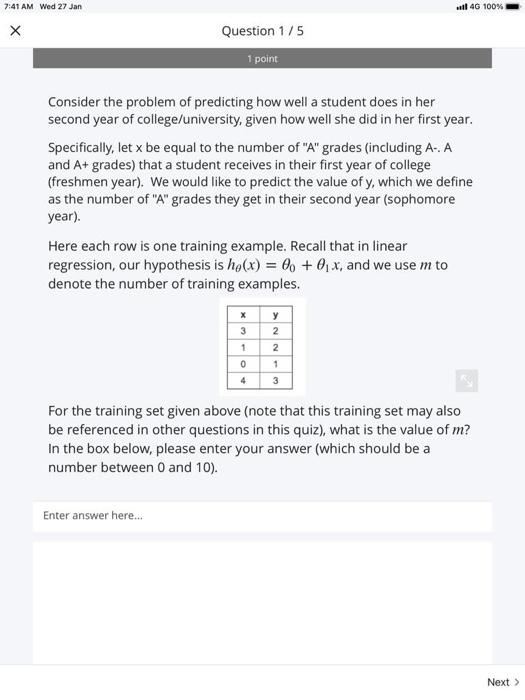
7:41 AM Wed 27 Jan wil 4G 100% Question 1/5 1 point Consider the problem of predicting how well a student does in her second year of college/university, given how well she did in her first year. Specifically, let x be equal to the number of "A" grades (including A- A and A+ grades) that a student receives in their first year of college (freshmen year). We would like to predict the value of y, which we define as the number of "A" grades they get in their second year (sophomore year) Here each row is one training example. Recall that in linear regression, our hypothesis is hp(x) = 0 + 01x, and we use m to denote the number of training examples. X y 2 3 1 2 0 1 For the training set given above (note that this training set may also be referenced in other questions in this quiz), what is the value of m? In the box below, please enter your answer (which should be a number between 0 and 10). Enter answer here... Next > 7:42 AM Wed 27 Jan 4G 100% Question 2/5 1 point Consider the following training set of m = 4 training examples: y 1 0.5 2 1 42 Consider the linear regression model ho(x) = 40 + 0, x. What are the values of C, and @, that you would expect to obtain upon running gradient descent on this model? (Linear regression will be able to fit this data perfectly.) O % = 0.5,01 = 0 O 0 = 1,01 = 1 O 0 = 0.5,01 = 0.5 O 0o = 0.01 = 0.5 O % = 1,01 = 0.5 7:42 AM Wed 27 Jan il 4G 100% Question 3/5 1 point Suppose we set 00 = -1,0 = 2 in the linear regression hypothesis from Q1. What is he(6)? Enter answer here... 7:42 AM Wed 27 Jan il 4G 100% Question 4/5 1 point Let f be some function so that f(0,0) outputs a number. For this problem, f is some arbitrary/unknown smooth function (not necessarily the cost function of linear regression, so f may have local optima). Suppose we use gradient descent to try to minimize f(0,01) as a function of Co and 6. Which of the following statements are true? (Check all that apply.) If @, and 6, are initialized so that to = 0, then by symmetry (because we do simultaneous updates to the two parameters), after one iteration of gradient descent, we will still have 0o = 0 Even if the learning rate a is very large, every iteration of gradient descent will decrease the value of f(0,01). f0o and 0, are initialized at a local minimum, then one iteration will not change their values. If the learning rate is too small, then gradient descent may take a very long time to converge 7:42 AM Wed 27 Jan il 4G 100% Question 5/5 1 point Suppose that for some linear regression problem (say, predicting housing prices as in the lecture), we have some training set, and for our training set we managed to find some 6.0, such that JO,0) = 0. Which of the statements below must then be true? (Check all that apply.) For these values of Co and that satisfy J(0,01) = 0, we have that he(x) = y for every training example (1) For this to be true, we must have 60 = 0 and 01 = 0 so that ho(x) = 0 This is not possible: By the definition of J(0.01), it is not possible for there to exist On and 0, so that 0,01) = 0 We can perfectly predict the value of y even for new examples that we have not yet seen. (eg, we can perfectly predict prices of even new houses that we have not yet seen.)