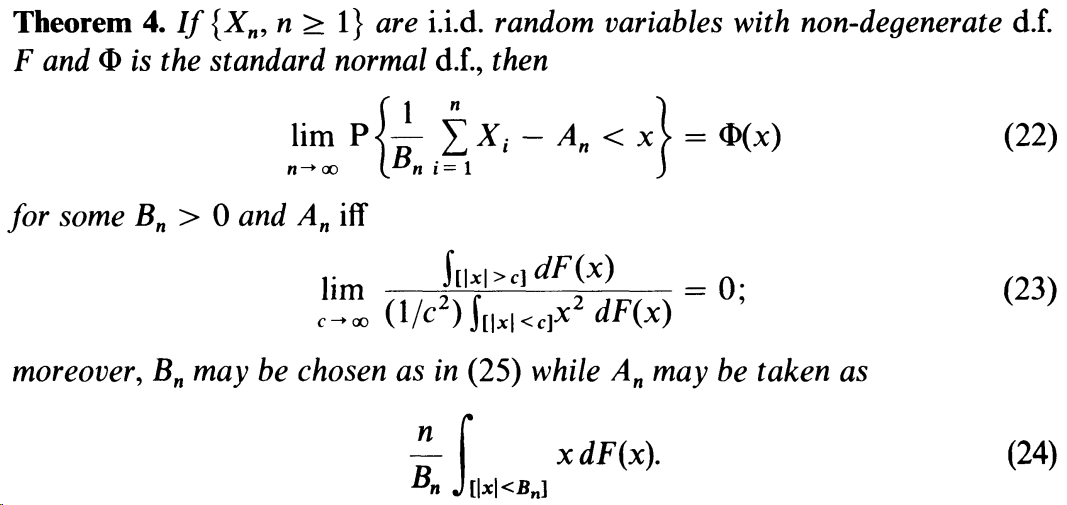
8. (i) For what positive values of , if any, does a C.L.T. hold for i.i.d. symmetric random variables with F(x): = 1 1/(2x), x 1, F(x) = , 0 x 1. - (ii) Does a C.L.T. hold for independent {X} with P{X = 1} = , P{X = n} 1/(2n), P{X = 0} = (1/2) (1/n)? = Hint: For part (i). You apply thm 4, and show in what condition of the fraction such that CLT holds. (So you got alpha > 2 part.) Then you consider when alpha = 2, and you will find whether CLT holds or not. For part (ii). You want to apply thm 1, and check whether Lindeberg condition holds or not. Then it is straightforward to see whether CLT holds Theorem 4. If {Xn, n 1} are i.i.d. random variables with non-degenerate d.f. F and is the standard normal d.f., then n lim P n 'n i=1 for some B > 0 and An iff lim C - An < x} = D(x) Sux > cj dF(x) (1/2)xx2 dF(x) = 0%; moreover, B, may be chosen as in (25) while A, may be taken as n n Br S xdF(x). [|x| Theorem 1 (Lindeberg). If {X, n 1} are independent random variables with zero means, variances {o}, and distribution functions {F} satisfying (2), then the distribution functions of the normalized sums S/s, tend to the standard normal. Conversely (Feller), convergence of these distribution functions to the standard normal and imply (2). - 0, Sn "S (4)