?

?

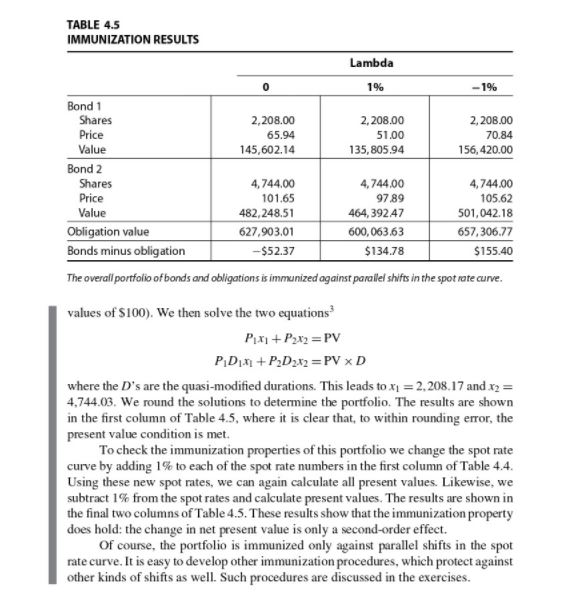
A company faces a stream of obligations over the next 8 years as shown: where the numbers denote thousands of dollars. The spot rate curve is that of Example 4.8. Try to find a portfolio, consisting of the two bonds described in that example, that has the same present value as the obligation stream and is immunized against an additive shift in the spot rate curve. Year 1 2 3 4 500 900 600 500 5 100 10 6 100 7 8 100 50 Example 4.8 (A million dollar obligation) Suppose that we have a $1 million obligation payable at the end of 5 years, and we wish to invest enough money today to meet this future obligation. We wish to do this in a way that provides a measure of protection against interest rate risk. To solve this problem, we first determine the current spot rate curve. A hypothetical spot rate curve s is shown as the column labeled spot in Table 4.4. We use a yearly compounding convention in this example in order to save space in the table. We decide to invest in two bonds described as follows: B is a 12-year 6% bond with price 65.95, and B is a 5-year 10% bond with price 101.66. The prices of these bonds are consistent with the spot rates; and the details of the price calculation are given in Table 4.4. The cash flows are multiplied by the discount factors (column d), and the results are listed and summed in columns headed PV and PV for the two bonds. We decide to immunize against a parallel shift in the spot rate curve. We cal- culate dP/dx, denoted by -PV' in Table 4.4, by multiplying each cash flow by t and by (1+)-(+) and then summing these. The quasi-modified duration is then the quotient of these two numbers; that is, it equals -(1/P)dP/d. The quasi-modified duration of bond 1 is, accordingly, 466/65.95=7.07. We also find the present value of the obligation to be $627.903.01 and the corresponding quasi-modified duration is 5/(1+ ss) = 4.56. To determine the appropriate portfolio we let x and x2 denote the number of units of bonds 1 and 2, respectively, in the portfolio (assuming, for simplicity, face TABLE 4.4 WORKSHEET FOR IMMUNIZATION PROBLEM Year 1 2345 d B 6 6 Spot 7.67 929 8.27 .853 8.81 .776 9.31 .700 9.75 628 10.16 560 10.52 496 10.85 439 11.15 386 339 11.42 11.67 297 11.89 6 6 6 6 6 6 6 6 6 PV 260 106 5.57 5.12 4.66 4.20 3.77 3.36 2.98 2.63 2.32 2.03 1.78 27.53 -PV 5 6 7 8 9 18.76 10 18.26 11 17.55 12 295.26 Total 466.00 Duration 7.07 The present values and durations of two bonds are found as transformations of cash flows. 65.95 5.18 9.45 12.84 15.38 17.17 18.29 18.87 18.99 B PV 10 9.29 10 8.53 10 7.76 10 7.00 110 69.08 101.66 -PV 8.63 15.76 21.40 25.63 314.73 386.15 3.80 TABLE 4.5 IMMUNIZATION RESULTS Bond 1 Shares Price Value Bond 2 0 2,208.00 65.94 145,602.14 4,744.00 101.65 482,248.51 627,903.01 -$52.37 Lambda 1% 2,208.00 51.00 135,805.94 4,744.00 97.89 464,39247 600,063.63 $134.78 -1% Shares Price Value Obligation value Bonds minus obligation The overall portfolio of bonds and obligations is immunized against parallel shifts in the spot rate curve. values of $100). We then solve the two equations Px + Px = PV PDx + PDX2=PV x D 2,208.00 70.84 156,420.00 4,744.00 105.62 501,042.18 657,306.77 $155.40 where the D's are the quasi-modified durations. This leads to x = 2,208.17 and x = 4,744.03. We round the solutions to determine the portfolio. The results are shown in the first column of Table 4.5, where it is clear that, to within rounding error, the present value condition is met. To check the immunization properties of this portfolio we change the spot rate curve by adding 1% to each of the spot rate numbers in the first column of Table 4.4. Using these new spot rates, we can again calculate all present values. Likewise, we subtract 1% from the spot rates and calculate present values. The results are shown in the final two columns of Table 4.5. These results show that the immunization property does hold: the change in net present value is only a second-order effect. Of course, the portfolio is immunized only against parallel shifts in the spot rate curve. It is easy to develop other immunization procedures, which protect against other kinds of shifts as well. Such procedures are discussed in the exercises.