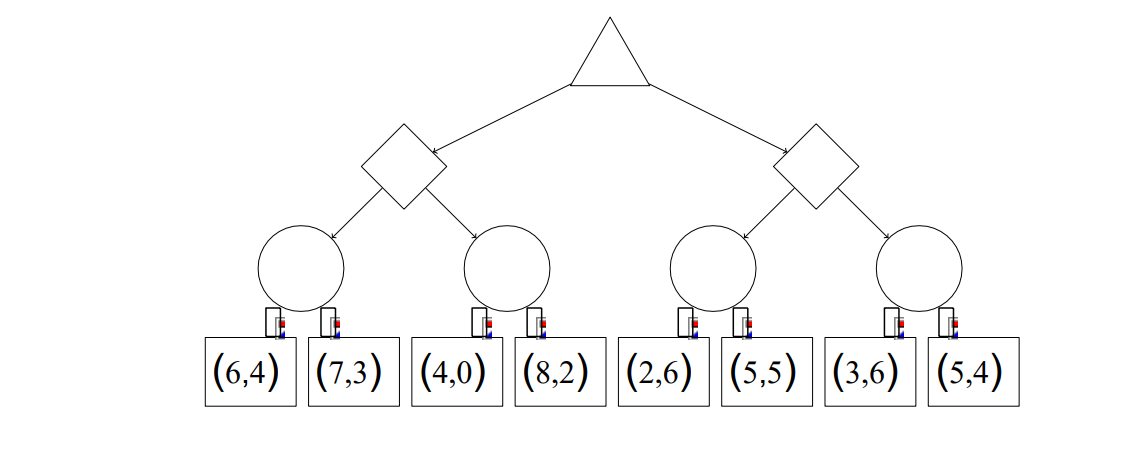
a ) [4 pts] Consider the following game tree for a two-player game. Each leaf node assigns a score to each player, in order (e.g. the leaf node (3, 1) corresponds to player 1 getting 3 points and player 2 getting 1 point).

Note that while player 1s goal is to maximize her own score, player 2s goal is to maximize his relative score (i.e. maximize the expression player 2s score minus player 1s score).

An upward-facing triangle represents a node for player 1, a diamond represents a node for player 2, and a circle represents a chance node (where either branch could be chosen with equal probability).

Fill in the values of all of the nodes; in addition, put an X on the line of all branches that can be pruned, or write No pruning possible below the tree if this is the case. Assume that branches are explored left-to-right.

(b) [4 pts] Based on the above strategies for each player, fill in the two sides of the inequality below with expressions using the below variables so that if the following inequality holds true, we can prune for player 2. If no pruning is ever possible in a search tree for this game, write No pruning possible. You may make reference to the following variables: 1 and 2 are the scores for the best option that any node for player 1 on the path from the root to the current node has seen, including the current node. 1 and 2 are the scores for the best option that any node for player 2 on the path from the root to the current node has seen, including the current node. (c) [4 pts] Player 1s and player 2s goals remain the same from the two previous parts. However, in this game, no pair of scores at a leaf node can have a sum greater than 10, and both players know this. Fill in the values of all of the nodes, and put an X on the line of all branches that can be pruned, or write No pruning possible below the tree if this is the case. Assume that branches are explored left-to-right.

(d) [4 pts] Taking into account this new information, fill in the two sides of the inequality below with expressions using the below variables so that if the following inequality holds true, we can prune for player 2. If no pruning is ever possible in a search tree for this game, write No pruning possible. You may make reference to the following variables: 1 and 2 are the scores for the best option that any node for player 1 on the path from the root to the current node has seen, including the current node. 1 and 2 are the scores for the best option that any node for player 2 on the path from the root to the current node has seen, including the current node.

a ) [4 pts] Consider the following game tree for a two-player game. Each leaf node assigns a score to each player, in order (e.g. the leaf node (3, 1) corresponds to player 1 getting 3 points and player 2 getting 1 point).

Note that while player 1s goal is to maximize her own score, player 2s goal is to maximize his relative score (i.e. maximize the expression player 2s score minus player 1s score).

An upward-facing triangle represents a node for player 1, a diamond represents a node for player 2, and a circle represents a chance node (where either branch could be chosen with equal probability).

Fill in the values of all of the nodes; in addition, put an X on the line of all branches that can be pruned, or write No pruning possible below the tree if this is the case. Assume that branches are explored left-to-right.

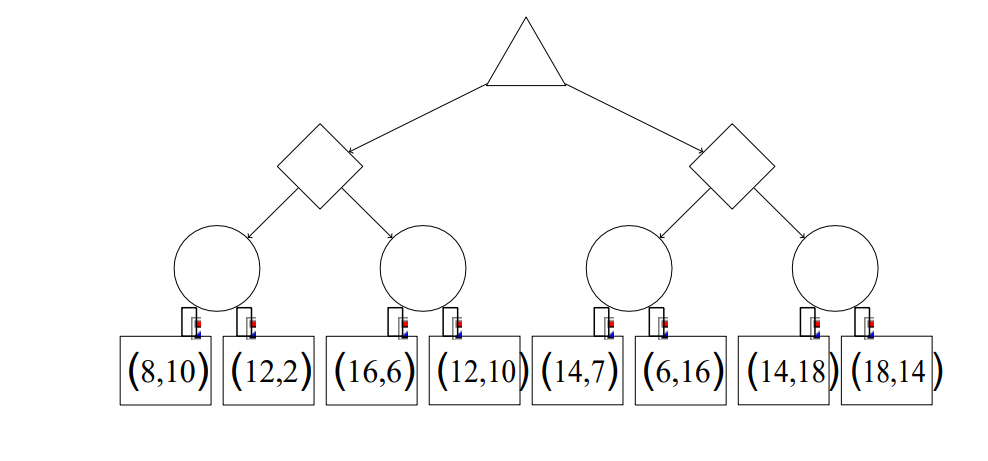
(b) [4 pts] Based on the above strategies for each player, fill in the two sides of the inequality below with expressions using the below variables so that if the following inequality holds true, we can prune for player 2. If no pruning is ever possible in a search tree for this game, write No pruning possible. You may make reference to the following variables: 1 and 2 are the scores for the best option that any node for player 1 on the path from the root to the current node has seen, including the current node. 1 and 2 are the scores for the best option that any node for player 2 on the path from the root to the current node has seen, including the current node. (c) [4 pts] Player 1s and player 2s goals remain the same from the two previous parts. However, in this game, no pair of scores at a leaf node can have a sum greater than 10, and both players know this. Fill in the values of all of the nodes, and put an X on the line of all branches that can be pruned, or write No pruning possible below the tree if this is the case. Assume that branches are explored left-to-right.

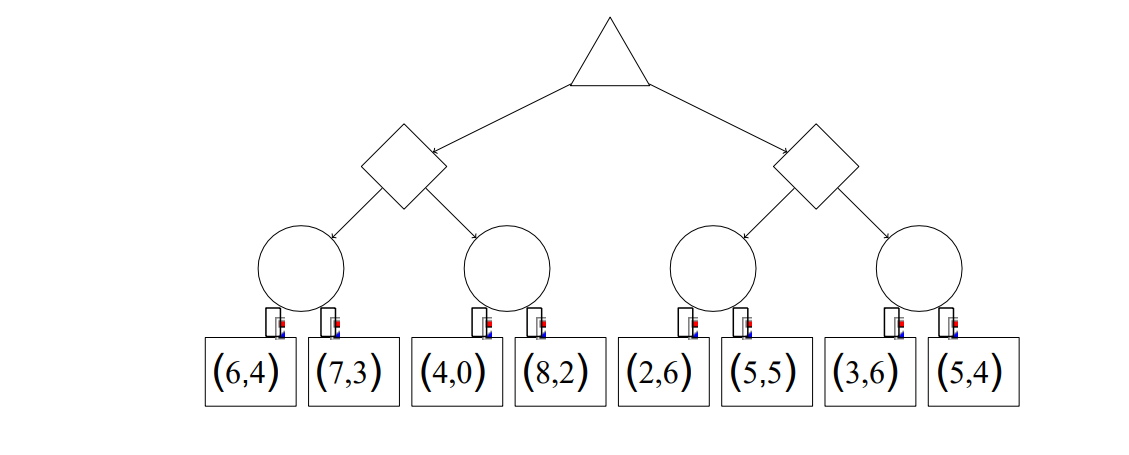
(d) [4 pts] Taking into account this new information, fill in the two sides of the inequality below with expressions using the below variables so that if the following inequality holds true, we can prune for player 2. If no pruning is ever possible in a search tree for this game, write No pruning possible. You may make reference to the following variables: 1 and 2 are the scores for the best option that any node for player 1 on the path from the root to the current node has seen, including the current node. 1 and 2 are the scores for the best option that any node for player 2 on the path from the root to the current node has seen, including the current node.