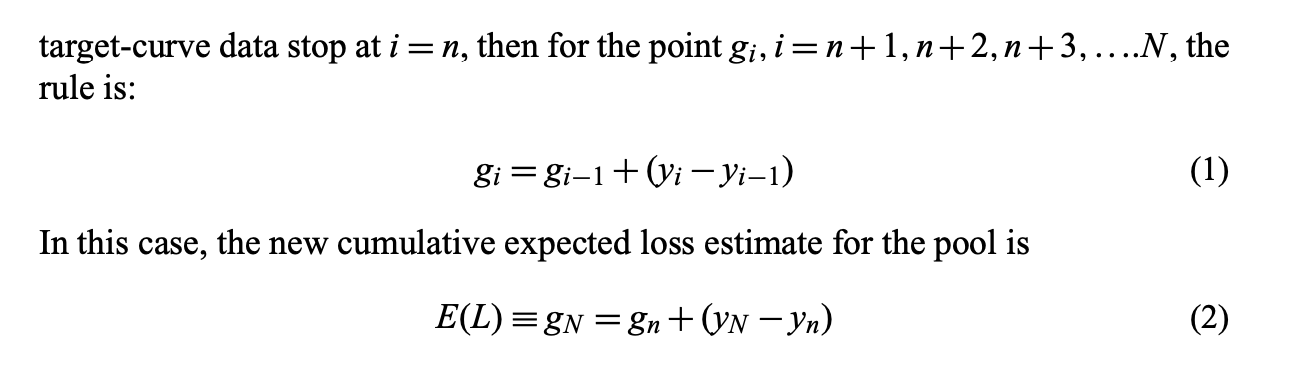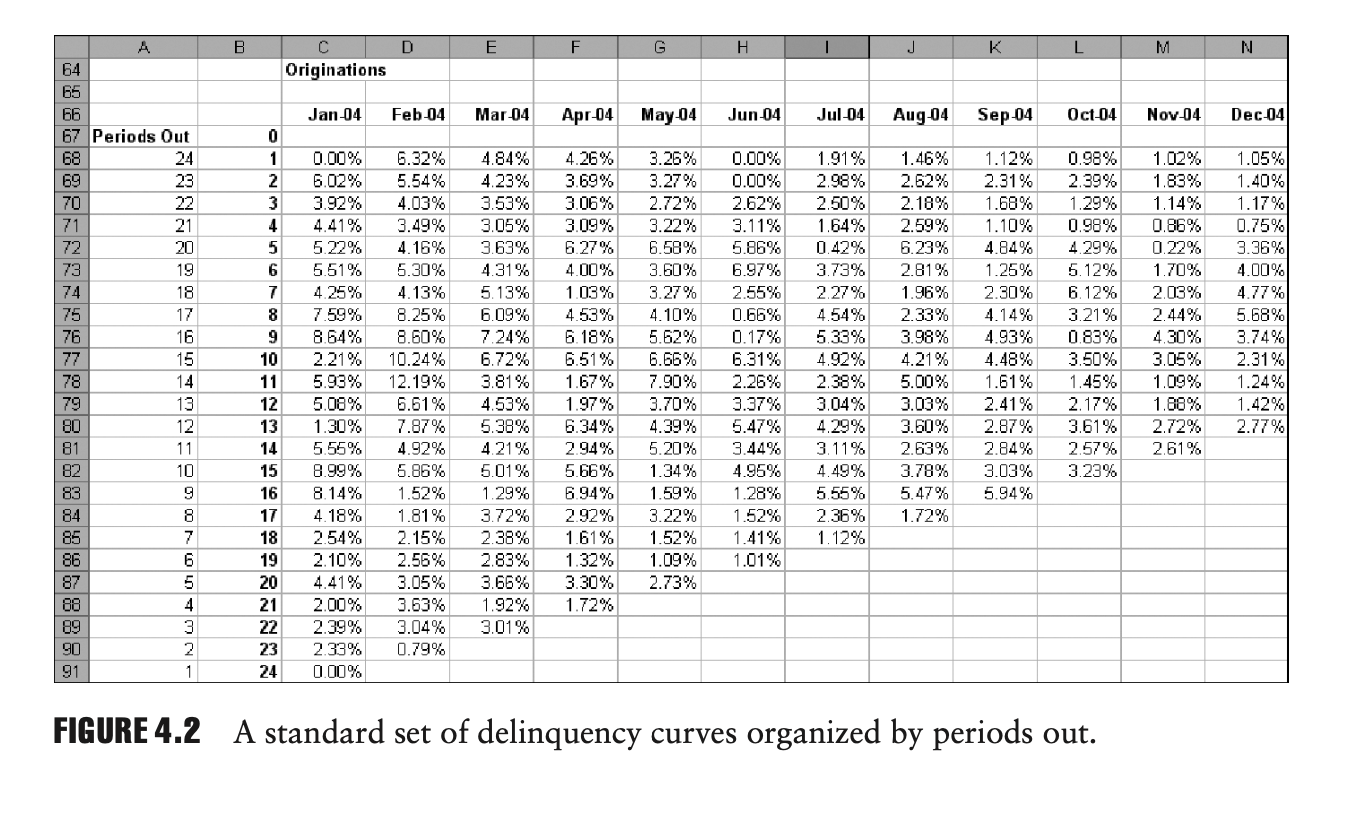
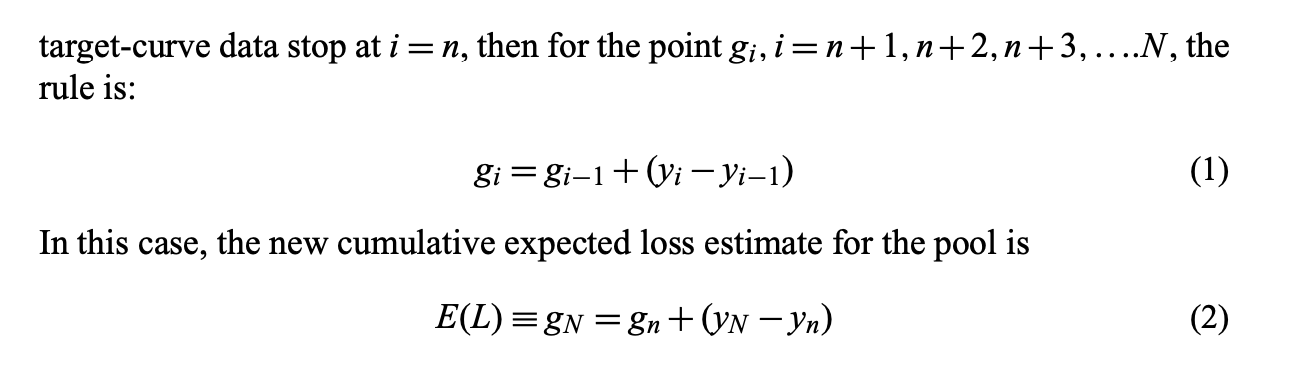
A B D E F G H I J K L M N C Originations Jan-04 Feb 04 Mar 04 Apr 04 May 04 Jun 04 Jul-04 Aug 04 Sep 04 Oct-04 Nov 04 Dec 04 67 Periods Out 0.00% 6.02% 3.92% 4.41% 5.22% 5.51% 4.25% 7.59% 8.64% 2.21% 5.93% .08% 1.30% 5.55% 8.99% 8.14% 4.18% 2.54% 2.10% 4.41% 2.00% 2.39% 2.33% 0.00% 6.32% 5.54% 4.03% 3.49% 4.16% 5.30% 4.13% 8.25% 8.60% 10.24% 12.19% 6.51% 7.87% 4.92% 5.86% 1.52% 1.81% 2.15% 2.56% 3.05% 3.63% 3.04% 0.79% 4.84% 4.23% 3.53% 3.05% 3.63% 4.31% 5.13% 6.09% 7.24% 6.72% 3.81% 4.53% 5.38% 4 21% 5.01% 1.29% 3.72% 2.38% 2.83% 3.66% 1.92% 3.01% 4.26% 3.69% 3.06% 3.09% 6.27% 4.00% 1.03% 4.53% 6.18% 6.51% 1.67% 1.97% 6.34% 2.94% 5.66% 6.94% 2.92% 1.61% 1.32% 3.30% 1.72% 3.26% 3.27% 2.72% 3.22% 6.58% 3.60% 3.27% 4.10% 5.62% 6.66% 7.90% 3.70% 4.39% 5.20% 1.34% 1.59% 3.22% 1.52% 1.09% 2.73% 0.00% 0.00% 2.62% 3.11% 5.86% 6.97% 2.55% 0.66% 0.17% 6.31% 2.26% 3.37% 5.47% 3.44% 4.95% 1.28% 1.52% 1.41% 1.01% 1.91% 2.98% 2.50% 1.64% 0.42% 3.73% 2.27% 4.54% 5.33% 4.92% 2.38% 3,04% 4.29% 3.11% 4.49% 5.55% 2.36% 1.12% 1.46% 2.62% 2.18% 2.59% 6.23% 2.81% 1.96% 2.33% 3.98% 4.21% 5.00% 3.03% 3.60% 2.63% 3.78% 5.47% 1.72% 1.12% 2.31% 1.68% 1.10% 4.84% 1.25% 2.30% 4.14% 4.93% 4.48% 1.61% 2.41% 2.87% 2.84% 3.03% 5.94% 0.98% 2.39% 1.29% 0.98% 4 29% 5.12% 6.12% 3.21% 0.83% 3.50% 1.45% 2.17% 3.61% 2.57% 3.23% 1.02% 1.83% 1.14% 0.86% 0.22% 1.70% 2.03% 2.44% 4 30% 3.05% 1.09% 1.88% 2.72% 2.61% 125 1.05% 1.40% 1.17% 0.75% 3.36% 4.00% 4.77% 5.68% 3.74% 2.31% 1.24% 1.42% 2.77% FIGURE 4.2 A standard set of delinquency curves organized by periods out. Multiplicative Method This is a ratio method whereby each new data point is set equal to the previous data point multiplied by the ratio of the target and previous data points for the base curve. Using the identical nomenclature, this rule is: gi = 8i-1 1 Yi-1 In that case, the new cumulative expected loss estimate for the pool is N Yi E(L)=gN=&ly E(L) =gn=gn i=n+1 Vi-1 target-curve data stop at i =n, then for the point gi, i=n+1,n+2,n+3, ....N, the rule is: gi =gi-1 +(yi Yi-1) In this case, the new cumulative expected loss estimate for the pool is E(L) =gn=gn +(YN Yn) Starting with MB4.2-Complete", from Chapter 4 in Allman, develop the alternative loss curve projections as proposed in R&R. Allman projects vintage loss curve data using the timing curve" method and R&R propose two alternatives called the "additive method" and the "multiplicative method", both described on page 88. Implement these methods and compare the results to Allman's method. What other alternative approaches might be proposed for generating a loss curve? A B D E F G H I J K L M N C Originations Jan-04 Feb 04 Mar 04 Apr 04 May 04 Jun 04 Jul-04 Aug 04 Sep 04 Oct-04 Nov 04 Dec 04 67 Periods Out 0.00% 6.02% 3.92% 4.41% 5.22% 5.51% 4.25% 7.59% 8.64% 2.21% 5.93% .08% 1.30% 5.55% 8.99% 8.14% 4.18% 2.54% 2.10% 4.41% 2.00% 2.39% 2.33% 0.00% 6.32% 5.54% 4.03% 3.49% 4.16% 5.30% 4.13% 8.25% 8.60% 10.24% 12.19% 6.51% 7.87% 4.92% 5.86% 1.52% 1.81% 2.15% 2.56% 3.05% 3.63% 3.04% 0.79% 4.84% 4.23% 3.53% 3.05% 3.63% 4.31% 5.13% 6.09% 7.24% 6.72% 3.81% 4.53% 5.38% 4 21% 5.01% 1.29% 3.72% 2.38% 2.83% 3.66% 1.92% 3.01% 4.26% 3.69% 3.06% 3.09% 6.27% 4.00% 1.03% 4.53% 6.18% 6.51% 1.67% 1.97% 6.34% 2.94% 5.66% 6.94% 2.92% 1.61% 1.32% 3.30% 1.72% 3.26% 3.27% 2.72% 3.22% 6.58% 3.60% 3.27% 4.10% 5.62% 6.66% 7.90% 3.70% 4.39% 5.20% 1.34% 1.59% 3.22% 1.52% 1.09% 2.73% 0.00% 0.00% 2.62% 3.11% 5.86% 6.97% 2.55% 0.66% 0.17% 6.31% 2.26% 3.37% 5.47% 3.44% 4.95% 1.28% 1.52% 1.41% 1.01% 1.91% 2.98% 2.50% 1.64% 0.42% 3.73% 2.27% 4.54% 5.33% 4.92% 2.38% 3,04% 4.29% 3.11% 4.49% 5.55% 2.36% 1.12% 1.46% 2.62% 2.18% 2.59% 6.23% 2.81% 1.96% 2.33% 3.98% 4.21% 5.00% 3.03% 3.60% 2.63% 3.78% 5.47% 1.72% 1.12% 2.31% 1.68% 1.10% 4.84% 1.25% 2.30% 4.14% 4.93% 4.48% 1.61% 2.41% 2.87% 2.84% 3.03% 5.94% 0.98% 2.39% 1.29% 0.98% 4 29% 5.12% 6.12% 3.21% 0.83% 3.50% 1.45% 2.17% 3.61% 2.57% 3.23% 1.02% 1.83% 1.14% 0.86% 0.22% 1.70% 2.03% 2.44% 4 30% 3.05% 1.09% 1.88% 2.72% 2.61% 125 1.05% 1.40% 1.17% 0.75% 3.36% 4.00% 4.77% 5.68% 3.74% 2.31% 1.24% 1.42% 2.77% FIGURE 4.2 A standard set of delinquency curves organized by periods out. Multiplicative Method This is a ratio method whereby each new data point is set equal to the previous data point multiplied by the ratio of the target and previous data points for the base curve. Using the identical nomenclature, this rule is: gi = 8i-1 1 Yi-1 In that case, the new cumulative expected loss estimate for the pool is N Yi E(L)=gN=&ly E(L) =gn=gn i=n+1 Vi-1 target-curve data stop at i =n, then for the point gi, i=n+1,n+2,n+3, ....N, the rule is: gi =gi-1 +(yi Yi-1) In this case, the new cumulative expected loss estimate for the pool is E(L) =gn=gn +(YN Yn) Starting with MB4.2-Complete", from Chapter 4 in Allman, develop the alternative loss curve projections as proposed in R&R. Allman projects vintage loss curve data using the timing curve" method and R&R propose two alternatives called the "additive method" and the "multiplicative method", both described on page 88. Implement these methods and compare the results to Allman's method. What other alternative approaches might be proposed for generating a loss curve