A baton is made of two large (identical) masses separated by a stick of length L. When thrown the baton twists and turns while it flies across space, and the motion of the baton's end appears very complicated to the observer. However, the physics allows the problem to be separated into two problems that you know (or will know soon):

1. The motion of the center of the baton (center of mass, a point mass), i.e. projectile motion.

2. The rotation of the end masses around the center of the baton (rotation assumed to be at constant angular velocity)

Thus at any point in time, one can find the ends of the baton, by considering the location of the center of mass, plus the rotation of the baton ends around the center (and the length of the baton) where :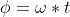

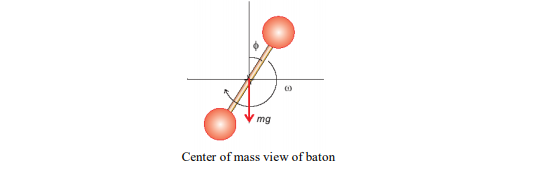
a) Write a python code that will calculate the path of the baton path (center), and the two ends of the baton (rotating around the center, with angular velocity ).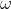

b) Make a plot of the trajectory (y vs. x) for the center and the baton ends.

c) Find (and plot) the velocity of the center, and both ends of the batons (linear velocity: plotting: vx vs. x and, vy vs. x).

Here are some values:

Earth's gravity: = 9.8 m/s^2

Entire baton mass: 0.5 kg

Baton Length: 0.5 m

Launch Angle: 30 degrees

Launch Velocity: 10.0 m/s

Angular velocity (spin rate): 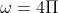rad/s

Time of flight: 0 through 1.75 sec

mg Center of mass view of baton mg Center of mass view of baton