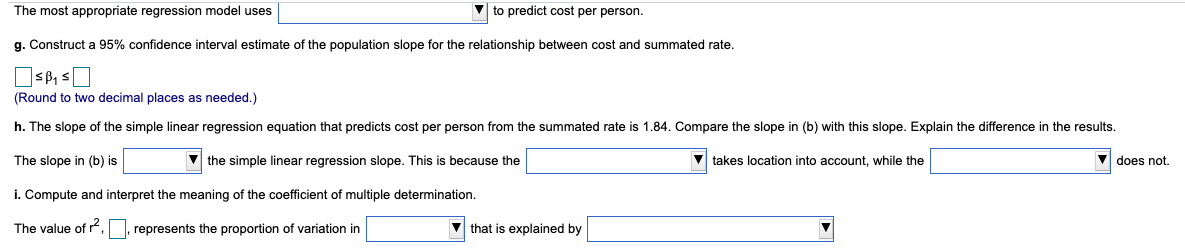
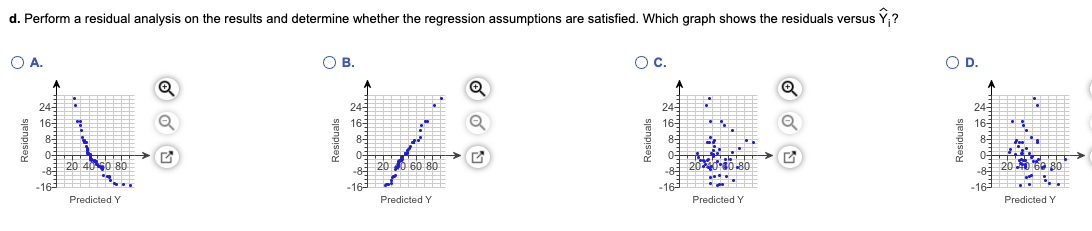
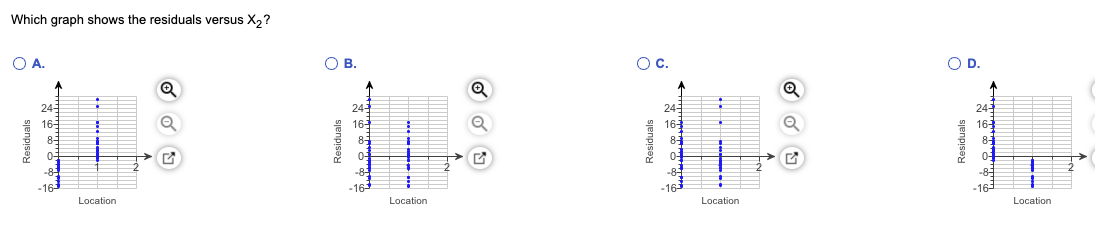
A company publishes restaurant ratings for various locations. The accompanying data table contains the summated rating for food, decor, service, and cost per person for a sample of 25 restaurants located in a city and 25 restaurants located in a suburb. Develop a regression model to predict the cost per person, based on the summated rating variable and a dummy variable concerning location (city versus suburban). Complete parts (a) through (p) below. For (a) through (1), do not include an interaction term. Click the icon to view the data set of restaurant ratings. a. State the multiple regression equation that predicts the cost per person, based on the summated rating, X,, and the location, X2. Define X2 to be 0 for restaurants located in a city and let X2 be 1 for restaurants located in a suburb. Y1 = 0+(0) X1 + ()X2i (Round to two decimal places as needed.) b. Interpret the regression coefficients in (a). Holding constant the effect of location of the restaurant, for each increase of 1 unit in the summated rating, the predicted cost per person is estimated to change by dollars. Holding constant the summated rating, the presence of the restaurant in a is estimated to decrease the predicted cost per person by | dollars over the cost per person of a restaurant in a Round to two decin 6 needed.)Deten'nine the pwalue. The pvalue is . (Round to three decimal places as needed.) State the condusion. Since the pvalue is V than the value at Ix, the null hypothesis. The rst independent variable, summated rating, Test the second independent variable, location. Determine the null and alternative hypotheses. \"0132 " H1132 ' {Tune inteners or decimals. Do not round.) to make a contribution to the regression model. Determine the test statistic. The test statistic is tSTAT = . {Round to M0 decimal places as needed.) Determine the pwalue. The pvalue is . (Round to three decimal places as needed.) State the condusion. Since the pvnlue is V than the value of or, Y the null hypothesis. The second independent variable, location, V to make a oontribmion to the regression model. The most appropriate regression model uses to predict cost per person. g. Construct a 95% confidence interval estimate of the population slope for the relationship between cost and summated rate. SB1 s (Round to two decimal places as needed.) h. The slope of the simple linear regression equation that predicts cost per person from the summated rate is 1.84. Compare the slope in (b) with this slope. Explain the difference in the results. The slope in (b) is the simple linear regression slope. This is because the takes location into account, while the does not. i. Compute and interpret the meaning of the coefficient of multiple determination. The value of re, , represents the proportion of variation in that is explained by1. Compute and interpret the adjusted re. The value of rid]! I: , represents the proportion of variation in {Round to three decimal places as needed.) that is explained by ll adjusted for k. The r2 value for the simple linear regression equation that predicts oost per person from the summated rate is 0.391. Compare the two r2 values. The r2 value for the multiple regression model is E the r2 value for the simple linear regression model. I. What conclusions can you reach about the effect of the summated rating and the location of the restaurant on the east of a meal? 'F the cost per person. " c. Predict the mean cost for a suburban restaurant with a summated rating of 50 and construct a 95% confidence interval estimate and a 95% prediction interval. The predicted mean cost is $ (Round to the nearest cent as needed.)d. Perform a residual analysis on the results and determine whether the regression assumptions are satisfied. Which graph shows the residuals versus Y;? O A. O B. O C. OD. 24 Residuals N N Residuals Residuals 16 20 40 50 80 20 0 60 80 80 Residuals 180 -16 -16 Predicted Y Predicted Y Predicted Y Predicted YWhich graph shows the residuals versus X, ? O A. O B. OC. O D. 24 24 24 24 Residuals 50 Residuals do Residuals 16 150 70 80 Residuals 50460 70 80 -163 -167 -164 -163 Summated Rating Summated Rating Summated Rating Summated RatingWhich graph shows the residuals versus X2? O A. OB. O c. OD. 24 Residuals Residuals 24 Residuals Residuals N -16- -16 Location Location -16 Location LocationAre the regression assumptions valid? Select all that apply. A. There is a pattern in the plot of residuals versus predicted values. The regression assumptions are not valid. B. There are no patterns in any of the residual plots. The regression assumptions are valid. C. There is a pattern in the plot of residuals versus X2. The regression assumptions are not valid. D. There is a pattern in the plot of residuals versus X, . The regression assumptions are not valid. e. Is there a significant relationship between price and the two independent variables (summated rating and location) at the 0.05 level of significance?e. Is there a significant relationship between price and the two independent variables (summated rating and location) at the 0.05 level of significance? What are the null and alternative hypotheses? O A. Ho: By #0 and B2 # 0 Hy : P1 = P2 = 0 OB. Ho: P1 = P2 = 0 Hy: P1 # 0 and B2 # 0 O C. Ho: At least one of B, and B2 is not 0. Hy : P1 = P2 =0 OD. Ho: P1 = P2 = 0Determine the test statistic. The test statistic is FSTAT = . (Round to two decimal places as needed.) Determine the pwalue. The pdvalue is . (Round to three decimal places as needed.) State the conclusion. Since the pvalue is F then the value of Int, Y the null hypothesis. There Y signicant relationship between the cost per person and the two independent variables. f. At the 0.05 level of significance, determine whether each independent variable makes a contribution to the regression model. Indicate the most appropriate regression model for this set of data. Test the first independent variable, summated rating. Determine the null and alternative hypotheses. Ho: P1 Hy : P1 (Type integers or decimals. Do not round.) Determine the test statistic. The test statistic is tSTAT =- (Round to two decimal places as needed.)