$($a$)$ Consider the modified problem

$\frac{d^{2}y}{d{t}^2}+2y^2\frac{dy}{dt}+4y=3sint,$ with $,y(0)=-1,\frac{dy}{dt}(0)=0.$

The ODE $(7)$ is very similar to $(4)$ except for the $y^2$ term in the left$-$hand side. Because of the

factor $y^2$ the ODE $(7)$ is nonlinear, while $(4)$ is linear. There is however very little to change

in the implementation of $(4)$ to solve $(7).$ In fact, the only thing that needs to be modified is

the ODE definition.

Modify the function defining the ODE in LAB$04$ex$1.$m$.$ Call the revised file LAB$04$ex$2.$m$.$ The

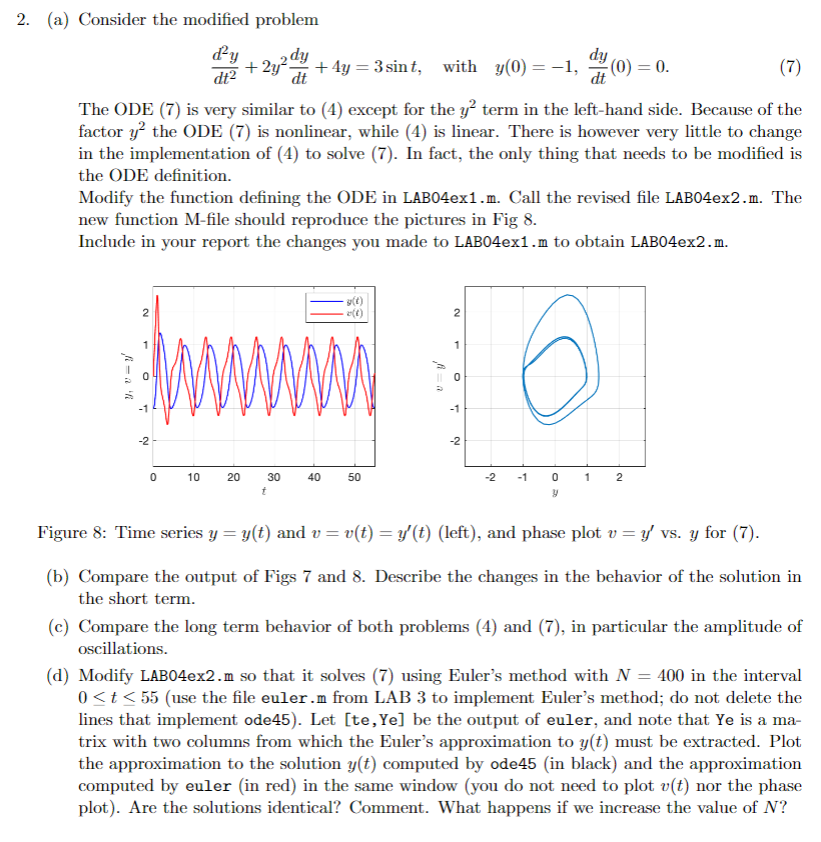
new function M$-$file should reproduce the pictures in Fig $8.$

Include in your report the changes you made to LAB$04$ex$1.$m to obtain LAB$04$ex$2.$m$.$

Figure $8$: Time series $y=y(t)$ and $v=v(t)=y^{\text{'}}(t)($left$),$ and phase plot $v=y^{\text{'}}$ vs$.y$ for $(7).$

$($b$)$ Compare the output of Figs $7$ and $8.$ Describe the changes in the behavior of the solution in

the short term.

$($c$)$ Compare the long term behavior of both problems $(4)$ and $(7),$ in particular the amplitude of

oscillations.

$($d$)$ Modify LAB$04$ex$2.$m so that it solves $(7)$ using Euler's method with $N=400$ in the interval

$0t55($use the file euler.m from LAB $3$ to implement Euler's method; do not delete the

lines that implement ode$45).$ Let $[$te$,$Ye$]$ be the output of euler, and note that Ye is a ma$-$

trix with two columns from which the Euler's approximation to $y(t)$ must be extracted. Plot

the approximation to the solution $y(t)$ computed by ode$45($in black$)$ and the approximation

computed by euler $($in red$)$ in the same window $($you do not need to plot $v(t)$ nor the phase

plot$).$ Are the solutions identical? Comment. What happens if we increase the value of $N?$