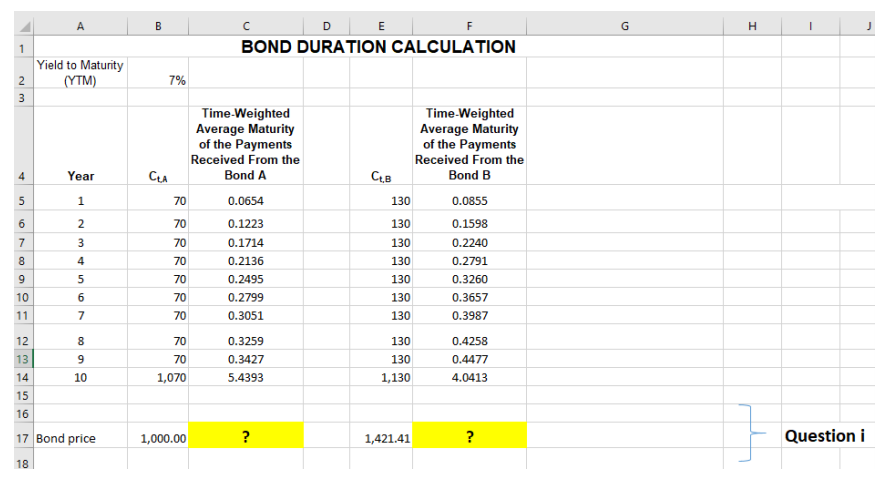
a) Consider two bonds A and B with payments , where , , , . Bond A has just been issued. Its face value is $1,000, it bears coupon rate of 7%, and it will mature in 10 years. Bond B was issued 5 years ago, when interest rates were higher.This bond has $1,000 face value and bears a 13% coupon rate. When issued, this bond had a 15-year maturity, so its remaining maturity is 10 years. The yield to maturity is 7% (see Cell B2).

i) Using the Excel spreadsheet below write down and explain the Excel formula on how we estimated the bond A and bond B price in Cells B17 and E17, respectively:

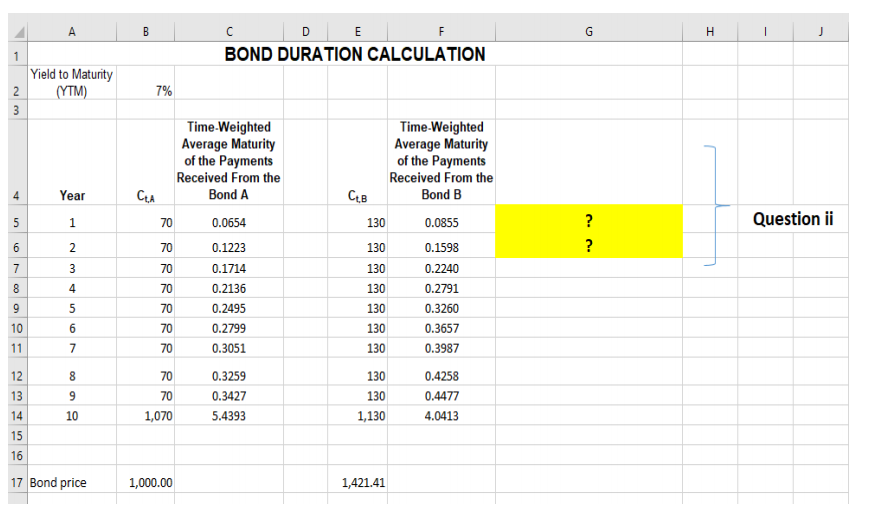
ii) Columns C and F in the Excel spreadsheet below report the time-weighted average maturity of the payments received from the Bond A and B, respectively. Write down and explain the Excel formula on how we estimated the values in Cells C5:C6 and F5:F6, respectively. Interpret those numbers.

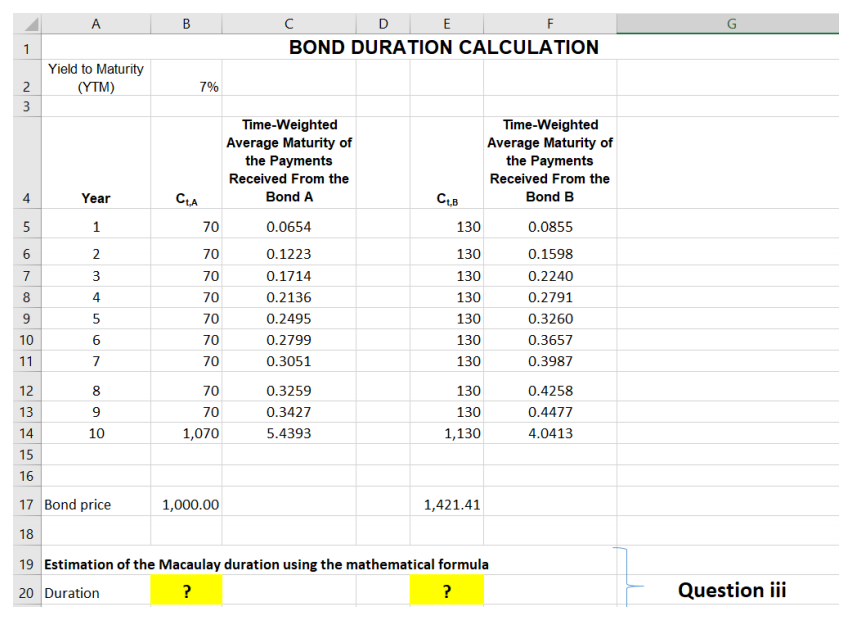
iii) Using the Excel spreadsheet below, estimate the duration of each of the two bonds A (Cell B20) and B (Cell E20), using the Macaulay duration measure. Which bond has the longest duration? Show your calculations and interpret your results.

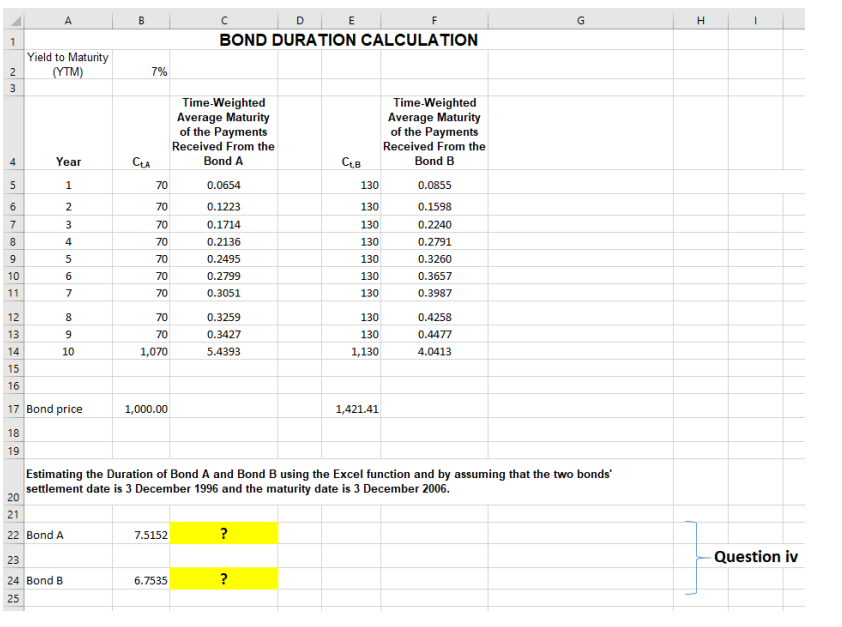
iv) Using the Excel spreadsheet below, write and explain the Excel formula on how we estimated the duration value of bond A and bond B in Cells B22 and B24, respectively, by assuming that the two bonds' settlement date is 3 December 1996, and the maturity date is 3 December 2006.

B E G H D BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 2 3 7% 4 Year CEA 5 1 Time-Weighted Average Maturity of the Payments Received From the Bond A 70 0.0654 70 0.1223 70 0.1714 70 0.2136 70 0.2495 70 0.2799 70 0.3051 Time-Weighted Average Maturity of the Payments Received From the CLB Bond B 130 0.0855 130 0.1598 130 0.2240 130 0.2791 130 0.3260 130 0.3657 130 0.3987 2 6 7 8 9 5 6 10 11 12 130 0.4258 13 14 15 9 10 70 70 1,070 0.3259 0.3427 5.4393 130 1,130 0.4477 4.0413 16 17 Bond price 1,000.00 ? 1,421.41 ? Question i 18 A B F G H DE BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 7% 2 3 Time-Weighted Average Maturity of the Payments Received From the Bond A Time-Weighted Average Maturity of the Payments Received From the Bond B 4 Year CA 5 1 130 ? Question ii 6 130 ? N 7 3 130 4 8 9 0.0654 0.1223 0.1714 0.2136 0.2495 0.2799 0.3051 130 0.0855 0.1598 0.2240 0.2791 0.3260 0.3657 0.3987 5 10 6 130 130 130 11 7 12 8 70 130 13 9 70 0.3259 0.3427 5.4393 130 0.4258 0.4477 4.0413 14 10 1,070 1,130 15 16 17 Bond price 1,000.00 1,421.41 A B E F D BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 7% 2 3 Time-Weighted Average Maturity of the Payments Received From the Bond A 70 0.0654 Time-Weighted Average Maturity of the Payments Received From the Bond B Year CLA CLB 4 5 5 1 130 6 3 4 7 8 9 10 11 70 70 70 70 70 70 0.1223 0.1714 0.2136 0.2495 0.2799 0.3051 130 130 130 130 130 130 0.0855 0.1598 0.2240 0.2791 0.3260 0.3657 0.3987 5 6 7 70 70 1,070 0.3259 0.3427 5.4393 130 130 1,130 0.4258 0.4477 4.0413 12 8 13 9 14 10 15 16 17 Bond price 18 1,000.00 1,421.41 19 Estimation of the Macaulay duration using the mathematical formula 20 Duration ? ? Question iii B G I E F BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 7% 2 3 4 Year 5 1 Time-Weighted Average Maturity of the Payments Received From the CA Bond A 70 0.0654 70 0.1223 70 0.1714 70 0.2136 70 0.2495 70 0.2799 70 0.3051 Time-Weighted Average Maturity of the Payments Received From the CB Bond B 130 0.0855 130 0.1598 130 0.2240 130 0.2791 130 0.3260 130 0.3657 130 0.3987 6 7 8 9 10 2 3 4 5 11 12 13 14 15 16 8 9 10 70 70 1,070 0.3259 0.3427 5.4393 130 130 1,130 0.4258 0.4477 4.0413 17 Bond price 1,000.00 1,421.41 18 19 Estimating the Duration of Bond A and Bond B using the Excel function and by assuming that the two bonds settlement date is 3 December 1996 and the maturity date is 3 December 2006. 20 21 22 Bond A 7.5152 ? Question iv 23 24 Bond B 25 6.7535 ? B E G H D BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 2 3 7% 4 Year CEA 5 1 Time-Weighted Average Maturity of the Payments Received From the Bond A 70 0.0654 70 0.1223 70 0.1714 70 0.2136 70 0.2495 70 0.2799 70 0.3051 Time-Weighted Average Maturity of the Payments Received From the CLB Bond B 130 0.0855 130 0.1598 130 0.2240 130 0.2791 130 0.3260 130 0.3657 130 0.3987 2 6 7 8 9 5 6 10 11 12 130 0.4258 13 14 15 9 10 70 70 1,070 0.3259 0.3427 5.4393 130 1,130 0.4477 4.0413 16 17 Bond price 1,000.00 ? 1,421.41 ? Question i 18 A B F G H DE BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 7% 2 3 Time-Weighted Average Maturity of the Payments Received From the Bond A Time-Weighted Average Maturity of the Payments Received From the Bond B 4 Year CA 5 1 130 ? Question ii 6 130 ? N 7 3 130 4 8 9 0.0654 0.1223 0.1714 0.2136 0.2495 0.2799 0.3051 130 0.0855 0.1598 0.2240 0.2791 0.3260 0.3657 0.3987 5 10 6 130 130 130 11 7 12 8 70 130 13 9 70 0.3259 0.3427 5.4393 130 0.4258 0.4477 4.0413 14 10 1,070 1,130 15 16 17 Bond price 1,000.00 1,421.41 A B E F D BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 7% 2 3 Time-Weighted Average Maturity of the Payments Received From the Bond A 70 0.0654 Time-Weighted Average Maturity of the Payments Received From the Bond B Year CLA CLB 4 5 5 1 130 6 3 4 7 8 9 10 11 70 70 70 70 70 70 0.1223 0.1714 0.2136 0.2495 0.2799 0.3051 130 130 130 130 130 130 0.0855 0.1598 0.2240 0.2791 0.3260 0.3657 0.3987 5 6 7 70 70 1,070 0.3259 0.3427 5.4393 130 130 1,130 0.4258 0.4477 4.0413 12 8 13 9 14 10 15 16 17 Bond price 18 1,000.00 1,421.41 19 Estimation of the Macaulay duration using the mathematical formula 20 Duration ? ? Question iii B G I E F BOND DURATION CALCULATION 1 Yield to Maturity (YTM) 7% 2 3 4 Year 5 1 Time-Weighted Average Maturity of the Payments Received From the CA Bond A 70 0.0654 70 0.1223 70 0.1714 70 0.2136 70 0.2495 70 0.2799 70 0.3051 Time-Weighted Average Maturity of the Payments Received From the CB Bond B 130 0.0855 130 0.1598 130 0.2240 130 0.2791 130 0.3260 130 0.3657 130 0.3987 6 7 8 9 10 2 3 4 5 11 12 13 14 15 16 8 9 10 70 70 1,070 0.3259 0.3427 5.4393 130 130 1,130 0.4258 0.4477 4.0413 17 Bond price 1,000.00 1,421.41 18 19 Estimating the Duration of Bond A and Bond B using the Excel function and by assuming that the two bonds settlement date is 3 December 1996 and the maturity date is 3 December 2006. 20 21 22 Bond A 7.5152 ? Question iv 23 24 Bond B 25 6.7535