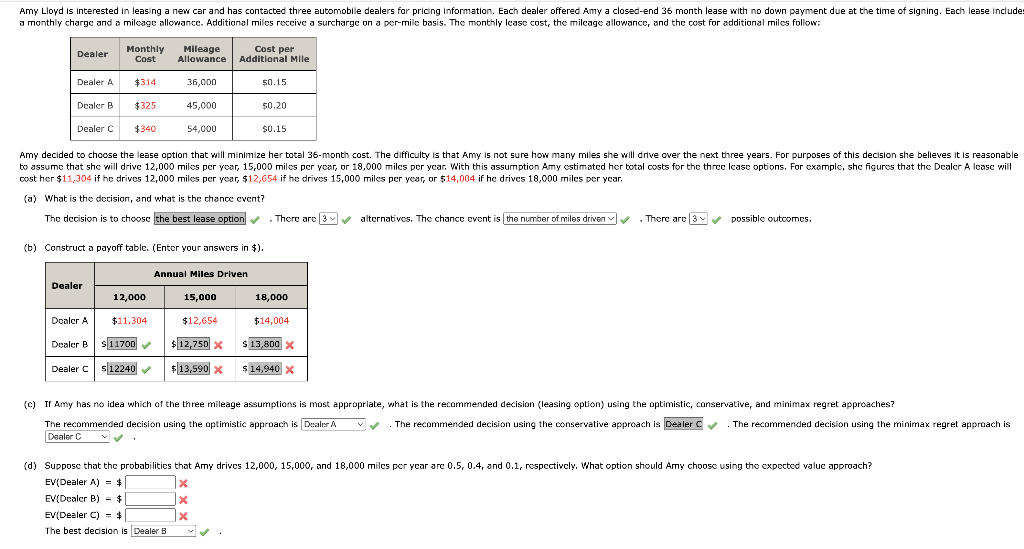
A) Construct a payoff table. (Enter your answers in $).
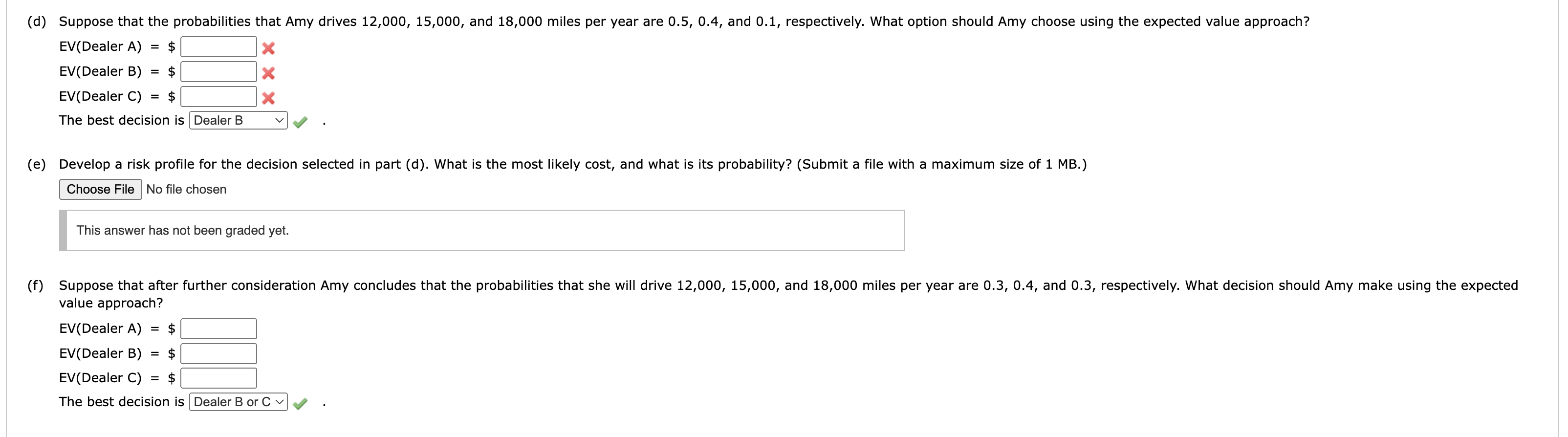
(d) Suppose that the probabilities that Amy drives 12,000, 15,000, and 18,000 miles per year are 0.5, 0.4, and 0.1, respectively. What option should Amy choose using the expected value approach?
EV dealer A:
Ev Dealer B:
Ev Dealer C:
E) Develop a risk profile for the decision selected in part (d). What is the most likely cost, and what is its probability?
(F)Suppose that after further consideration Amy concludes that the probabilities that she will drive 12,000, 15,000, and 18,000 miles per year are 0.3, 0.4, and 0.3, respectively. What decision should Amy make using the expected value approach?
EV Dealer A
Ev Dealer B
Ev dealer C
sorry for a) it is to develop a risk profile instead
cost her $11,304 if he drives 12,000 miles per year, $12,654 if he drives 15,000 miles per year, or $14,004 if he drives 18,000 miles per year. (a) What is the decision, and what is the chance cvent? The decision is to cheose . There are alternatives. The chance event is . There are possible outcomes. (b) Construct a payoff table. (Enter your answers in $ ). The recommended decision using the aptimistic approach is . The recommended decision using the conservative approach is . The recommended decision using the minimax regret appraach is EV(DealerA)=$EV(DealerB)=$Ev(DealerC)=$Thebestdecionis The best decision is (d) Suppose that the probabilities that Amy drives 12,000,15,000, and 18,000 miles per year are 0.5,0.4, and 0.1 , respectively. What option should Amy choose using the expected value approach? EV(DealerA)=$ EV(DealerB)=$EV(DealerC)=$ The best decision is (e) Develop a risk profile for the decision selected in part (d). What is the most likely cost, and what is its probability? (Submit a file with a maximum size of 1 MB.) No file chosen This answer has not been graded yet. value approach? EV( Dealer A)=$ EV( Dealer B)=$ EV( Dealer C)=$ The best decision is Dealer B or C cost her $11,304 if he drives 12,000 miles per year, $12,654 if he drives 15,000 miles per year, or $14,004 if he drives 18,000 miles per year. (a) What is the decision, and what is the chance cvent? The decision is to cheose . There are alternatives. The chance event is . There are possible outcomes. (b) Construct a payoff table. (Enter your answers in $ ). The recommended decision using the aptimistic approach is . The recommended decision using the conservative approach is . The recommended decision using the minimax regret appraach is EV(DealerA)=$EV(DealerB)=$Ev(DealerC)=$Thebestdecionis The best decision is (d) Suppose that the probabilities that Amy drives 12,000,15,000, and 18,000 miles per year are 0.5,0.4, and 0.1 , respectively. What option should Amy choose using the expected value approach? EV(DealerA)=$ EV(DealerB)=$EV(DealerC)=$ The best decision is (e) Develop a risk profile for the decision selected in part (d). What is the most likely cost, and what is its probability? (Submit a file with a maximum size of 1 MB.) No file chosen This answer has not been graded yet. value approach? EV( Dealer A)=$ EV( Dealer B)=$ EV( Dealer C)=$ The best decision is Dealer B or C








