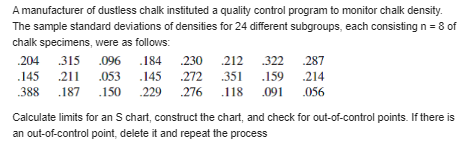
A control chart for thickness of rolled-steel sheets is based on an upper control limit of .0520 in. and a lower limit of .0475 in. The first ten values of the quality statistic (in this case X. , the sample mean thickness of n = 5 sample sheets) are .0506, _0493, .0502, .0501, .0512, .0498, 0485, .0500, _0505, and .0483. Construct the initial part of the quality control chart, and comment on its appearance.Consider the control chart based on control limits , + 2.81 or/v. a. What is the ARL when the process is in control? b. What is the ARL when n = 4 and the process mean has shifted to p = Up + 0? c. How do the values of parts (a) and (b) compare to the corresponding values for a 3-sigma chart?Refer to Exercises 8 and 9, and now employ control limits based on using the sample ranges to estimate o. Does the process appear to be in control? Reference Exercises 8 The table below gives data on moisture content for specimens of a certain type of fabric. Determine control limits for a chart with center line at height 13.00 based on o = .600, construct the control chart, and comment on its appearance. O = .600, Reference Exercises 9 Refer to the data given in Exercise 8, and construct a control chart with an estimated center line and limits based on using the sample standard deviations to estimate o. Is there any evidence that the process is out of control?A manufacturer of dustless chalk instituted a quality control program to monitor chalk density. The sample standard deviations of densities for 24 different subgroups, each consisting n = 8 of chalk specimens, were as follows: 204 .315 .096 .184 230 .212 .322 .287 145 .211 .053 .145 .272 .351 .159 .214 .388 .187 .150 .229 .276 .118 .091 -056 Calculate limits for an S chart, construct the chart, and check for out-of-control points. If there is an out-of-control point, delete it and repeat the process\fSome sources advocate a somewhat more restrictive type of doubling-sampling plan in which r = G + 1; that is, the lot is rejected if at either stage the (total)) number of defectives is at least r (see the book by Montgomery). Consider this type of sampling plan with n, = 50, n, = 100, G, = 1, and r, = 4. Calculate the probability of lot acceptance when p = _02, 05, and .10.\f