A cookie manufacturer has two warehouses W₁ and W₂, from which identical boxes of cookies are to be shipped to n stores S_i, for i = 1,...,n. Let s_i be the number of boxes of cookies ordered by S_i, for i = 1,...,n, and w₁,w₂ be the numbers of boxes of cookies available at W₁,W₂, respectively. Assume that there are exactly enough boxes of cookies available to fill the orders, i.e., w₁ +w₂ = 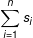. Let c_ki be the cost of shipping one box of cookies from W_k to S_i, for k = 1, 2 and i = 1, . . . , n. To minimize the shipping cost, the cookie manufacturer wishes to determine the actual number of boxes of cookies to send from W_k to S_i, denoted by x_ki for k=1,2 and i=1,...,n such that:

the order made by S_i is filled, i.e., x_1i+x_2i = s_i, fori=1,...,n

the inventory at W_k is exactly sufficient, i.e., 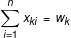, for k = 1,2

and the total shipping cost, 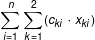, is minimized.

Question (a): Let g(j, x) be the cost incurred when W₁ has an inventory of x boxes of cookies and the cookies are sent to store S_i for i = 1,...,j in the optimal manner. Write a recursive definition for g(j, x).

(Note that W₂ is not mentioned because knowledge of the inventory for W₁ implies knowledge of the inventory for W₂ since w1 + w2 = 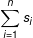. i.e., if y is the inventory available at W₂, then )

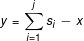Question (b): Use this recurrence to devise a dynamic programming algorithm to compute the minimum shipping cost to fill all orders.