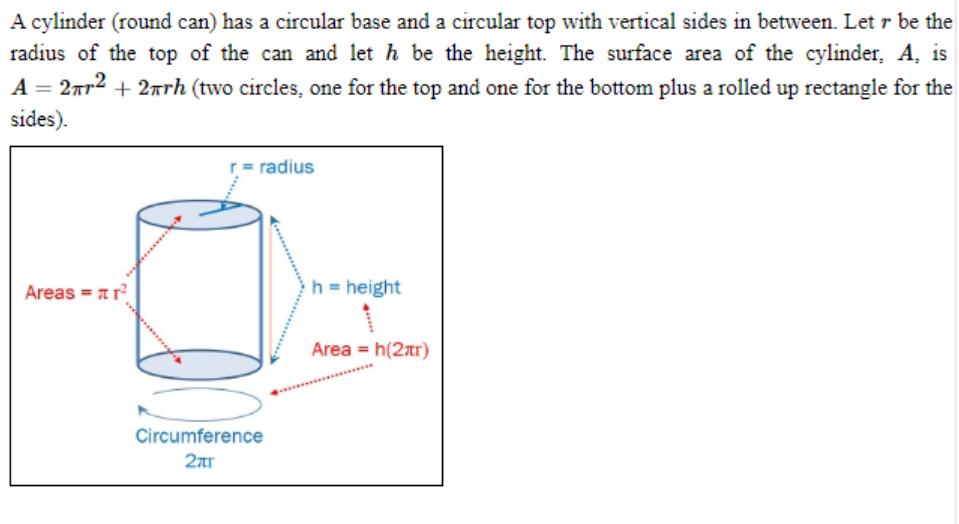
A cylinder (round can) has a circular base and a circular top with vertical sides in between. Let r be the radius of the top of the can and let h be the height. The surface area of the cylinder, A, is A = 2r2 + 2arh (two circles, one for the top and one for the bottom plus a rolled up rectangle for the sides). Areas = r = radius Circumference 2 h = height ***** Area = h(2r) Part a: Assume that the height of your cylinder is 6 inches. Consider A as a function of r, so we can write that as A (r) = 2 + 12 r. What is the domain of A (r)? In other words, for which values of r is A (r) defined? Part b: Continue to assume that the height of your cylinder is 6 inches. Write the radius r as a function of A. This is the inverse function to A (r), i.e., to turn A as a function of r into r as a function of A. T (A) =