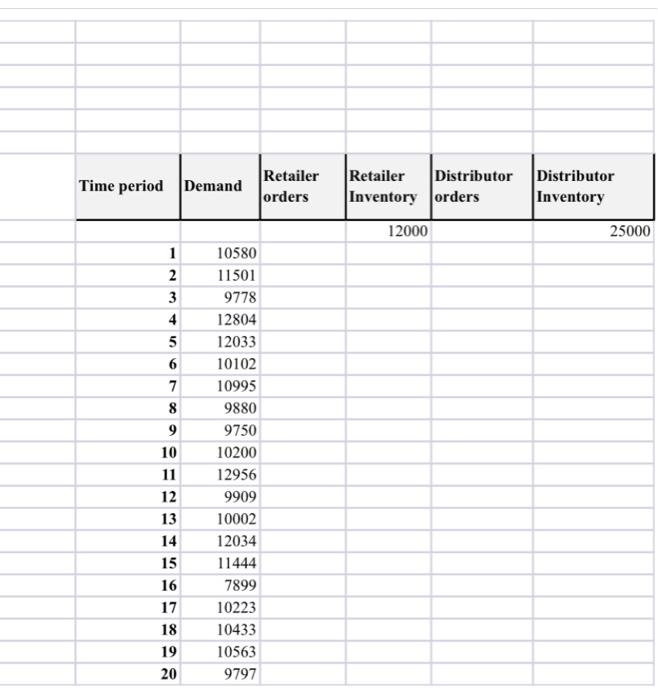
A diaper manufacturer, DiaperCo, is experiencing high variability in the volume of incoming orders from a distributor for a particular SKU. This causes problems for DiaperCo -- aggregate planning becomes difficult, and there is a large risk of overage as well as underage in every planning period. The manufacturer suspects the high variability is due to the bullwhip effect. The distributor receives incoming orders from a retailer. Initial discussions with the distributor indicate that it is also experiencing high variability in incoming orders, although not as high as the manufacturer. Owing to this, Diaperco wants to explore how different ordering behaviors from the retailer and the distributor affect variability in the orders it receives. Since stabilizing the order pattern would lead to lower costs, the retailer has agreed to share its 20-period demand forecast with DiaperCo as long as any future cost reductions also lead to lower prices. A forecast for the demand faced by the retailer is given in this Excel-file. Both the retailer and the distributor use a 20-period rolling horizon when planning how much to order Assume the following sequence of events at both the retailer and the distributor. In the beginning of a period, they review inventory and decide how much to order. Orders are placed and arrive immediately, and can be sold in the same period. Time period Demand Retailer orders Retailer Distributor Inventory orders Distributor Inventory 12000 25000 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 10580 11501 9778 12804 12033 10102 10995 9880 9750 10200 12956 9909 10002 12034 11444 7899 10223 10433 10563 9797 Part 1 0.0/5.0 points (graded) DiaperCo learns that, as of now, both the retailer and the distributor use (S,Q)- policies, where all orders have the same quantity Q. The retailer and the distributor each use the EOQ formula to find the order quantity, using the forecasted demand for the next 20 periods. The holding cost for the 20 periods is $1 per unit for the retailer, and $0.5 per unit for the distributor. The ordering cost is $1,000 for the retailer and $2,000 for the distributor. For both the retailer and the distributor, an order is placed when the inventory on hand in the beginning of a period is below certain level, S. This level is given by the average sales in a period plus a safety stock. For the retailer, the safety stock is 5,000 units. For the distributor the safety stock is 10,000 units. DiaperCo wants to measure the "size" of bullwhip effect as the ratio between the variance in incoming orders (to DiaperCo) over the variance of the demand. Using EOQ ordering at both the retailer and the distributor, what is the size of the bullwhip effect at DiaperCo? Answer without commas or decimals. Note. The formula of the Economic Order Quantity (EOQ) is EOQ = 1 24D Where is the ordering cost, D the demand, and ce the excess holding cost. For more information about the EOQ see Key Concepts Document in the handouts section. A diaper manufacturer, DiaperCo, is experiencing high variability in the volume of incoming orders from a distributor for a particular SKU. This causes problems for DiaperCo -- aggregate planning becomes difficult, and there is a large risk of overage as well as underage in every planning period. The manufacturer suspects the high variability is due to the bullwhip effect. The distributor receives incoming orders from a retailer. Initial discussions with the distributor indicate that it is also experiencing high variability in incoming orders, although not as high as the manufacturer. Owing to this, Diaperco wants to explore how different ordering behaviors from the retailer and the distributor affect variability in the orders it receives. Since stabilizing the order pattern would lead to lower costs, the retailer has agreed to share its 20-period demand forecast with DiaperCo as long as any future cost reductions also lead to lower prices. A forecast for the demand faced by the retailer is given in this Excel-file. Both the retailer and the distributor use a 20-period rolling horizon when planning how much to order Assume the following sequence of events at both the retailer and the distributor. In the beginning of a period, they review inventory and decide how much to order. Orders are placed and arrive immediately, and can be sold in the same period. Time period Demand Retailer orders Retailer Distributor Inventory orders Distributor Inventory 12000 25000 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 10580 11501 9778 12804 12033 10102 10995 9880 9750 10200 12956 9909 10002 12034 11444 7899 10223 10433 10563 9797 Part 1 0.0/5.0 points (graded) DiaperCo learns that, as of now, both the retailer and the distributor use (S,Q)- policies, where all orders have the same quantity Q. The retailer and the distributor each use the EOQ formula to find the order quantity, using the forecasted demand for the next 20 periods. The holding cost for the 20 periods is $1 per unit for the retailer, and $0.5 per unit for the distributor. The ordering cost is $1,000 for the retailer and $2,000 for the distributor. For both the retailer and the distributor, an order is placed when the inventory on hand in the beginning of a period is below certain level, S. This level is given by the average sales in a period plus a safety stock. For the retailer, the safety stock is 5,000 units. For the distributor the safety stock is 10,000 units. DiaperCo wants to measure the "size" of bullwhip effect as the ratio between the variance in incoming orders (to DiaperCo) over the variance of the demand. Using EOQ ordering at both the retailer and the distributor, what is the size of the bullwhip effect at DiaperCo? Answer without commas or decimals. Note. The formula of the Economic Order Quantity (EOQ) is EOQ = 1 24D Where is the ordering cost, D the demand, and ce the excess holding cost. For more information about the EOQ see Key Concepts Document in the handouts