$($a$)$

For the purpose of this question, consider a "vertex rearranging function" for a graph G $=($V$,$ E$)$ is a function $\backslash$phi : V $->$ V that rearranges the vertices of G while preserving the graph's structure. This means that if there is an edge between vertices u and v in G$,$ then there must also be an edge between $\backslash$phi $($u$)$ and $\backslash$phi $($v$)$ in G$,$ and if there is no edge between u and v$,$ then there is none between $\backslash$phi $($u$)$ and $\backslash$phi $($v$).$ In other words, $\backslash$phi is a bijective map from V to V such that $($u$,$v$)$ in E implies $(\backslash$phi $($u$),\backslash$phi $($v$))$ in E and $($u$,$v$)$ E implies $(\backslash$phi $($u$),\backslash$phi $($v$))$ E$.$

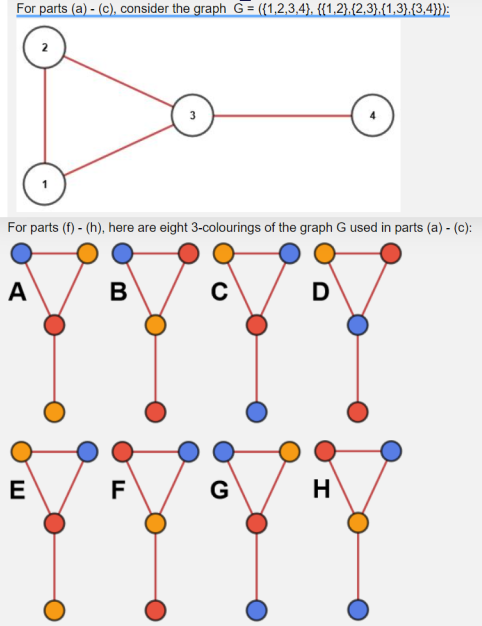
Show that the graph G $=(\{1,2,3,4\},\{\{1,2\},\{2,3\},\{1,3\},\{3,4\}\})($shown in the stimulus on the left$)$ only has one possible non$-$trivial $($that doesn't simply map each vertex to itself$)$ 'vertex rearranging function' as defined above.$($b$)$

How many $3-$colourings does the graph from part $($a$)$ have? $($Hint: there are at least $8)$

Justify your answer $($though partial marks are available for correct answers without justification$)($c$)$

We are given $8$ possible $3-$colourings of our graph G from part $($a$).($shown in the stimulus on the left$).$

Find another possible $3-$colouring.$($d$)$

Consider an arbirary graph G $=($V$,$ E$)$ where V is the set of vertices and E is the set of edges. Let C be a set of colours.

Let ColG be the set of all colourings of vertices of G by colours from C$.$ That is$,$

ColG $=\{\backslash$alpha :V $->$ C such that $\backslash$alpha is a valid colouring of G $\}$

Define a relation R$1$ ColG $\backslash$times ColG as follows:

$(\backslash$alpha $,\backslash$beta $)$ in R$1$ if and only if there exists a bijection f:C$->$C such that for all v in V$,$ f$(\backslash$alpha $($v$))=\backslash$beta $($v$)$

Prove that R$1$ is an equivalence relation.We say two colourings $\backslash$alpha : V$->$C and $\backslash$beta : V $->$ C are equivalent under permutation of colours if $(\backslash$alpha $,\backslash$beta $)$ in R$1.($e$)$

With ColG as defined in $($d$),$ define the relation R$2$ ColG $\backslash$times ColG as follows:

$(\backslash$alpha $,\backslash$beta $)$ in R$2$ if and only if there exists a vertex rearrangement function $($see $($a$))$

$\backslash$phi : V $->$ V such that for all v in V$,\backslash$alpha $($v$)=\backslash$beta $(\backslash$phi $($v$)).$

This is to say, one coloring can be transformed into the other by rearranging the vertices according to $\backslash$phi while keeping the colors assigned to each vertex the same.

Prove that R$2$ is an equivalence relation.$($f$)$

Consider the $8$ colourings $($A$-$H$)$ of the graph from part $($a$)$ shown on the left.

Draw the directed graph with

vertices are these $8$ colourings $($do not include the extra one you found in $($c$))$; and

edges are given by the relation R$1.($g$)$

Consider the $8$ colourings $($A$-$H$)$ of the graph from part $($a$)$ shown on the left.

Draw the directed graph with

vertices are these $8$ colourings $($do not include the extra one you found in $($c$))$; and

edges are given by the relation R$2.($h$)$

How do R$$ and R$$ partition the set of colourings $\{$A$,...,$ H$\}$ respectively?$($i$)$

Consider the directed graph obtained by associating each vertex to a colouring and adding an edge between two vertices $\backslash$alpha and $\backslash$beta if $(\backslash$alpha $,\backslash$beta $)$ in R$\backslash$cup R$.$

We define two colourings $\backslash$alpha and $\backslash$beta as being distinct when there does not exist a path between $\backslash$alpha and $\backslash$beta on said graph.

How many colourings in A$-$H are distinct?