A good application of the time value of money is the lottery problem. If you won a $6 million lottery, would you take the lump sum or annuitize it over 20 years? The article below addresses that issue. After reading it and applying the principles from time value of money in the readings and homework problems, answer the following questions and post your responses in this forum. Also respond to at least two other postings on this discussion.

1) If you were given the choice of receiving the lump sum from the lottery in the article or the 20-year annuity, which would you take? Justify your response in terms of time value analysis or other financial or nonfinancial considerations.

2) In the appendix to the article, an article from local financial experts made their recommendations on another lottery. What mistakes can you identify in their analyses?

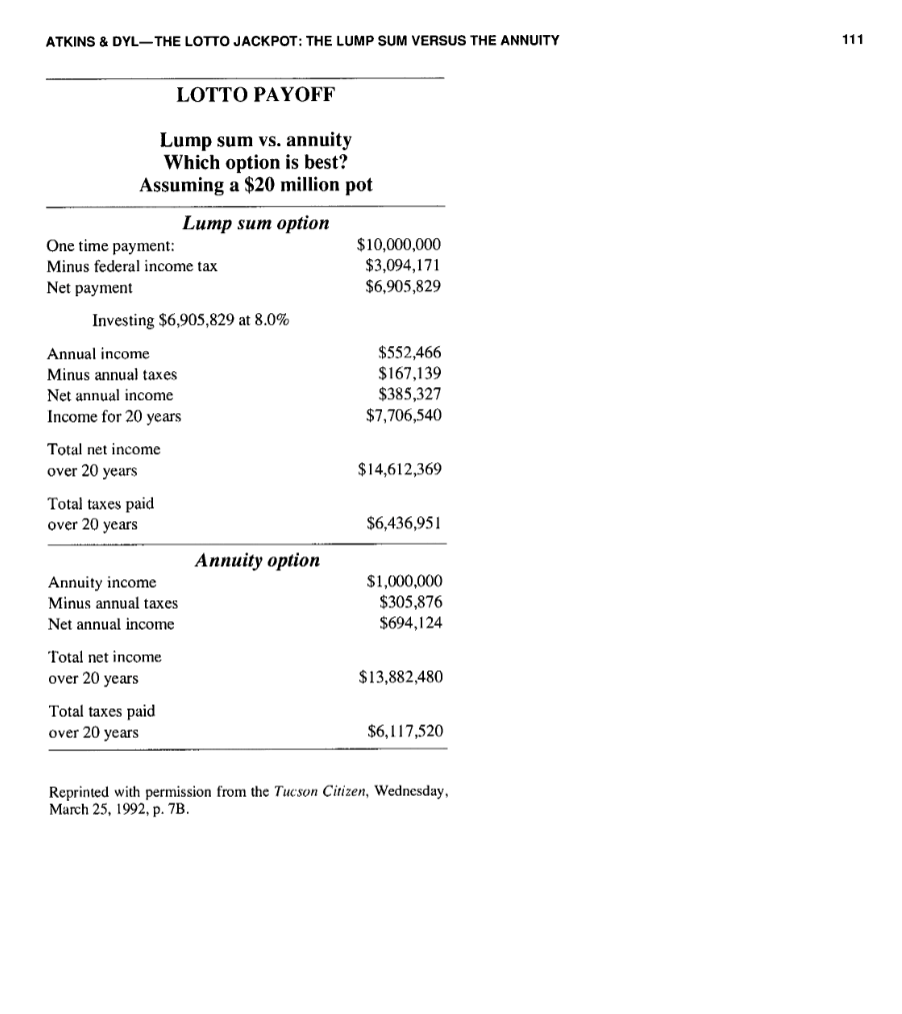The Lotto Jackpot: The Lump Sum Versus the Annuity Allen B. Atkins and Edward A. Dyl Lotto players who win the jackpot must choose to receive their winnings as either an annuity or a lump sum. Students in an introductory finance class can determine the best alternative, applying their knowledge of present value and tax considerations to an interesting "real world" financial decision. Using the current lottery in your state further piques the students' interest. The lump sum payment is taxed immediately, whereas the annuity payments are taxed when they are received. Analysis of a $6,000,000 jackpot shows the annuity netting the winner $686,899 more than the lump sum. - Most state Lotto games (and many other lotteries) offer the winner of the jackpot a choice between an annuity due of twenty annual payments or a lump sum equal to the present value of the twenty-year annuity. Which altemative should the winner choose? This is not an unreasonable question to pose to students taking their first course in finance. Although their analyses may not be perfect, the excrcise is a leaming experience they will remember. As background, in a standard Lotto, a percentage of the revenue from ticket sales for a particular drawing is allocated to a prize pool and the remainder of the money is used to fund various state projects. The advertised size of the jackpot is the sum of the annual annuity payments that the lottery officials estimate they will be able to pay with the money in the prize pool, with no adjustment for the time value of money. If the winner chooses the annuity, several insurance companies bid on the right to pay the twenty-year annuity. State lottery officials pay the amount in the prize pool to the company whose bid provides the largest annuity payment to the Lotto winner. The insurance company with the best bid usually offers a return approximating the rate on long-term United States Treasury Bonds. A winner who chooses the Lump Sum simply receives the prize pool that would have been used to purchase the annuity. Back to our question: Which alternative should the winner choose? When Lotto was first introduced in Arizona, the headline of an article in the Arizona Daily Star stated, "Lump-sum Lotto payout is best bet, experts say." 1 Is this Allen B. Atkins is Assistant Professor of Finance. Edward A. Dyl is Professor of Finance. Both are at the University of Arizona,Tuscon, AZ 85721 . 'The "experts" were some local CPAs. A similar article is shown in the appendix. This particular article is an excellent class handout. Challenge your students to see how many errors are in the analysis. really true? We present a simple method to evaluate the lump sum versus annuity decision. Most of your students will employ some variant of this approach (we hope) in their analysis of the problem. Highlighting the differences in their answers is a good way to launch the classroom discussion. We also compute the interest rate the winner earns on the annuity versus the lump sum, illustrating why most players should probably select the annuity. Although the annuity is more valuable, most winners in Arizona select the lump sum payment. Either they do not understand how to analyze the problem or their choice is motivated by non-financial considerations. This lottery problem is especially effective when the current lottery jackpot is used to pose the question. We suggest the instructor buy a lottery ticket where you have to choose between a lump sum payment and an annuity. Show them the ticket and tell them the estimated jackpot. Students enjoy discovering that their new-found knowledge about finance has made them more knowledgeable than both the general public and some so-called experts. In the classroom discussion, they learn that advertised prizes do not necessarily equal present values. In addition, the calculations dramatically demonstrate the importance of tax considerations. Finally, the students' interest in the problem is always quite high, resulting in a lively discussion. I. The Lump Sum Versus Annuity Decision The proper way to analyze this decision is to compare the after-tax proceeds from the lump sum to the present value of the annual, after-tax, cash flows from the annuity. The preferred alternative may vary among individuals. It depends 108 FINANCIAL PRACTICE \& EDUCATION_FALL/WINTER 1995 on their tax rate, their estimate of the interest rate, and of course, non-financial factors. Although it is most effective to use the current Lotto jackpot in your state as the classroom problem-making the problem of immediate interest and distinguishing it from the usual hypothetical exercises-here we use a $6,000,000 jackpot as an illustration. The students must understand that the advertised jackpot is merely an estimate of the sum of the annuity payments that can be made given the estimated prize pool. Usually Lotto players do not know the value of the prize pool and so the instructor must either provide the students with an estimate of the lump sum or require them to estimate this amount based on the advertised jackpot. Panel A in Exhibit 1 shows the computation of the after-tax proceeds from winning a $6,000,000 Lotto jackpot. First, we estimate the value of the prize pool by computing the present value of a twenty-year annuity due with annual payments of $300,000. That is, when Lotto advertises a $6,000,000 jackpot (20$300,000), the amount in the prize pool is the present value of a $300,000 annuity at current interest rates. To estimate this amount, we use a discount rate of 8.0%, roughly the yield on long-term government bonds at the time of our calculation. This present value can be found using either the formula for the present value of an annuity due shown in Exhibit 1 or a financial calculator. 2 We estimate that the advertised $6,000,000 jackpot will pay the winner a lump sum of $3,181,080. The first step in the students' analysis is to compute the after-tax value of the lump sum. We use (and recommend) the simplifying assumption that the winner has no other income. The federal income tax is $75,304.50 plus 39.6% of the amount over $250,000.3 Our illustration assumes an average state income tax rate of 5.0%.4 After subtracting the federal tax of $1,236,012 and the state tax of $159,054, the winner is left with $1,786,014,5 roughly 30% of the 2 Some textbooks no longer show the formula for the present value of an annuity due. The formula is simply the present value of an annuity for t1 years: (1(1+r)11)/r with the number 1 added to it. The number 1 represents the payment to be received at time t=0, which, of course, requires no discounting. 3 We assume the taxpayer is marricd and filing a joint return. The first $38,000 of taxable income is taxed at a rate of 15%, the next bracket applies to income up to $91,850 and is taxed at 28%, the third bracket applies to income up to $140,000 and is taxed at 31% and the fourth bracket applies to income up to $250,000 and is taxed at 36%. All amounts over $250,000 are taxed at 39.6%. The 1994 tax rate schedule can be found in the instruction booklet for the IRS form 1040 . 4he details of each state's tax code could be employed in the analysis, but telling the students the highest marginal tax rate is probably sufficient. 5 The Arizona lottery withholds only 24% for Federal and state taxes, but this is irrelevant. The taxes that must be paid are the relevant consideration, not the taxes that are withheld by the lottery. A winner must pay all or his or her taxes. advertised jackpot. The instructor must decide whether to mention taxes or simply to hope that the students will incorporate income taxes in their analyses. This choice depends on your knowledge of the students' capabilities and your pedagogical objectives for this exercise. Determining the present value of the annuity is the next step in the students' analysis. This procedure is illustrated in Panel B of the exhibit. They must first determine the after-tax cash flow from the annuity, which is simply the before-tax cash flow ( $300,000 in this case) minus the federal and state taxes. This leaves the winner with $189,895 per year for twenty years with the first payment occurring at t=0. The next step is to choose an interest rate to use in the analysis. The students must recognize that they are comparing two riskless alternatives-the lump sum and the annuity due. We use the current rate on long-term United States Treasury securities, a before-tax interest rate of 8.0% in our example. This interest rate is used to compute the after-tax discount rate, which is simply the interest rate times one minus the two tax rates. In our example, the average federal tax rate is 31.7% and the average state tax rate is 5.0%. Obviously, it is important to use an after-tax discount rate to value after-tax cash flows. We find that the after-tax interest rate is 5.064%. Why do we use a before-tax rate to compute the value of the lump sum and an after-tax rate to compute the value of the annuity? Because the actual amount of the annual annuity is determined by the insurance company, which sells the annuity. They use the before-tax rate in calculating what they are willing to pay given the value of the prize pool. In contrast, the jackpot winner must discount the after-tax payments he or she will receive by the after-tax rate (the opportunity cost) to find the present value of that stream of income. The final step in the students' analysis is to compute the present value of the after-tax cash flows from the annuity. This present value is the amount of money the winner would require today to duplicate exactly the cash flows promised by the annuity at a given interest rate. This figure is directly comparable to the after-tax proceeds from the lump sum payment. The decision rule is simple: Take the larger amount. In our example, the present value of the annuity is $2,472,913, which is substantially more than the $1,786,014 value of the lump sum payment. In this case, the correct financial decision is to take the annuity! Two caveats are in order. First, remember that different individuals may have different interest rates. Consider someone who is deeply in debt and is paying an interest rate of 18% on the debt. This person should probably use a before-tax interest rate of 18% (which is an after-tax rate of 11.39% ) to evaluate the annuity. The value of the annuity to ATKINS \& DYL-THE LOTTO JACKPOT: THE LUMP SUM VERSUS THE ANNUITY Exhibit 1. Formulas for Valuing a " $6,000,000 " LOTTO Jackpot Panel A. Value of the Lump Sum DiscountRateforLottoJackpot=0.08EstimatedValueofthePrizePool=Payment[1+(1(1+r)19)/r]=300,000[1+(10.23171)/0.08]=300,00010.6036=3,181,080 After-TaxValueoftheLumpSum=LumpSumFederalTax-StateTax3,181,080(75,304.50+(LumpSum250,000)(0.396))(LumpSum)(0.05)=3,181,080(75,304.50+(3,181,080250,000)(0.396))(3,181,080)(0.05)=3,181,0801,236,012159,054=1,786,014 Panel B. Value of the Annuity After-TaxCashFlowBefore-TaxInterestRateAfter-TaxDiscountRatePresentValue=AnnuityFederalTaxStateTax=Annuity(75,304.50+(Annuity250,000)(0.396))(Annuity)(0.05)=300,000(75,304.50+(300,000250,000)(0.396))(300,000)(0.05)=300,00095,10515,000=189,895=i=0.08=r=i(1AverageFederalTaxRateAverageStateTaxRate)i(10.3170.05)=0.08(0.633)=0.05064=CashFlow[1+(1(1+r)19)/r]=189,895[1+(10.391179)/0.05064]=189,89513.02253=2,472,913 this person is $1,642,364, which is slightly less than the value of the lump sum. This individuals should take the $1,786,014 lump sum and pay off his or her debts. Second, the choice between the lump sum and the annuity may not be merely a financial decision. For example, if you don't plan to live for twenty years and you don't like your heirs, take the money and spend it! The instructor can usually generate an interesting and pedagogically useful discussion of each of these two issues. II. The Effective Interest Rate Why is the annuity such a good deal? Basically, the effective yield that provides the annuity in our example is 8.0%. That is, the $300,000 per year is a return of 8.0% on $3,181,080. This doesn't sound like a huge return. However, a winner would need to earn a rate of return of 19.5% on the $1,786,014 net after-tax proceeds from the lump sum payment to duplicate the $300,000 per year from the annuity-very few safe investments promise an 19.5% return. How is the State able to offer such a good deal? Taxes! When the State gives the lottery winner a lump sum of $3,181,080, the winner must pay his or her taxes immediately and has only $1,786,014 to invest. When the State buys the annuity for the winner, the State invests the full before-tax amount of $3,181,080. The winner defers the tax until each annuity payment is received. The longer the money can be invested before the government collects its taxes, the more the jackpot winner can earn. This is analogous to an investor who invests for capital gains over current income. Taxes on the capital gains are deferred until the investment is sold, whereas taxes on the current income are paid out each year. III. Conclusion We illustrate a method for valuing the annuity alternative available from the Lotto. The value of the annuity depends 110 FINANCIAL PRACTICE \& EDUCATION_FALL/WINTER 1995 on the winner's tax rate and on the after-tax retum that could be earned by investing the lump sum. When the present value of the after-tax cash flows from the annuity is larger than the after-tax value of the lump sum payment, select the annuity. On a purely financial basis, the annuity option is probably the best choice for most individuals. Why, then, do most winners take the lump sum? It is possible that the after-tax annual payment of $189,895 does not make the winner feel as "rich" as a one time payment of $1,786,014. That "rich" feeling is expensive, however, costing the winner $686,899($2,472,913$1,786,014) in the present value of his or her assets. The instructor in an introductory finance class can use this example to enhance the students' interest. Undergraduate students frequently have had few personal experiences where financial analysis is relevant. Most are interested in the Lotto, however, and this helps to make the analysis fascinating to them. Again, don't use our example as merely another class problem. Use the "real" lottery jackpot that's reported in your local newspaper. Appendix: To Lump or Not to Lump: Lotto Payout Method Depends on Investment Smarts By Jennifer Boice Citizen Business Editor Should you take the lump sum if you win the new Lotto game? The best that local financial planners would advise was "it depends." It depends on how savvy an investor you are. It depends on what you want to accomplish. And it depends on how old you are."Personally," said The Conservative Investor's Bob Swift, "I would take it all up front. Because then I'd be in control. I can do much better on an annual return than the state is offering." At current rates, the state would invest the money--probably about $10 million if someone wins today-and buy an 8 percent annuity, paying the winner $20 million over the 20 years. That's about $1 million a year-less about $305,000 in state and federal taxes. If you could invest the money at a greater than 8 percent total return, you would be better off than if the state invested the money for you, planners said. But can you be trusted with the lump sum? "The benefit of paying it out in an annuity is, you can't blow it," said Jane Rojas, vice president of investments with Kemper Securities in Tucson. "Someone with no prior knowledge or investment experience should take the annuity," she advised. Beth Vance, financial planner with IDS Financial Services, agreed. "There are so many stories about widows who receive then lose their insurance money. I can't imagine what kind of phone calls someone who learned they had $6 million would get." But then again, said Vance, "If it was me, I'd take the lump sum. I could eam better than 8 percent." Also, if you are old, planners said, there's no need to have payments stretching over 20 years. What about taxes? Either choice, the Arizona Lottery withholds some taxes-20 percent federal, 4 percent state-before you even see the money. However, you will have to fork over another roughly 15 percent in state and federal taxes to pay your entire bill, said David Peachin, partner with KPMG Peat Marwick in Tucson. Plus, on any income you earn from investments, or-if by slim chance you still kept one-your job, you will have to pay the top tax rate-about 39 percent state and federal combined-on that money, too. Crunching the numbers, Gail Williams, an accountant with Alpha Tax Services, found that by taking the lump sum, you would end up with more money-about $1 million more over a 20-year period. She used a very simple scenario: A single person, with no other income, who doesn't reinvest any of the yearly income. That person electing to take the lump sum could invest the after-tax total-about $6.9 million-in an 8 percent Treasury bond. He or she would end up earning a total of about $14.6 million after taxes over 20 years, with an annual income of $552,000 to blow. Electing to take the annuity, the annual income would be almost $700,000, but over 20 years, the winner would have a total of $13.8 million after taxes to spend. By taking the annuity, the winner also would be paying annual income taxes on a larger annual income and chances are those taxes in the future will be higher, not lower. "I was right," said Williams. "Looking at the numbers shows you probably should take the lump sum." ATKINS \& DYL-THE LOTTO JACKPOT: THE LUMP SUM VERSUS THE ANNUITY Keprinted with permission trom the t ucson citizen, weanesaay, March 25, 1992, p. 7B