A graph is an abstract structure of objects $($called vertices$)$ and connections

among them $($called edges$)$ that can be used to model any network of

connected objects. There are many measures of network complexity that

are useful in understanding properties of the entire network.

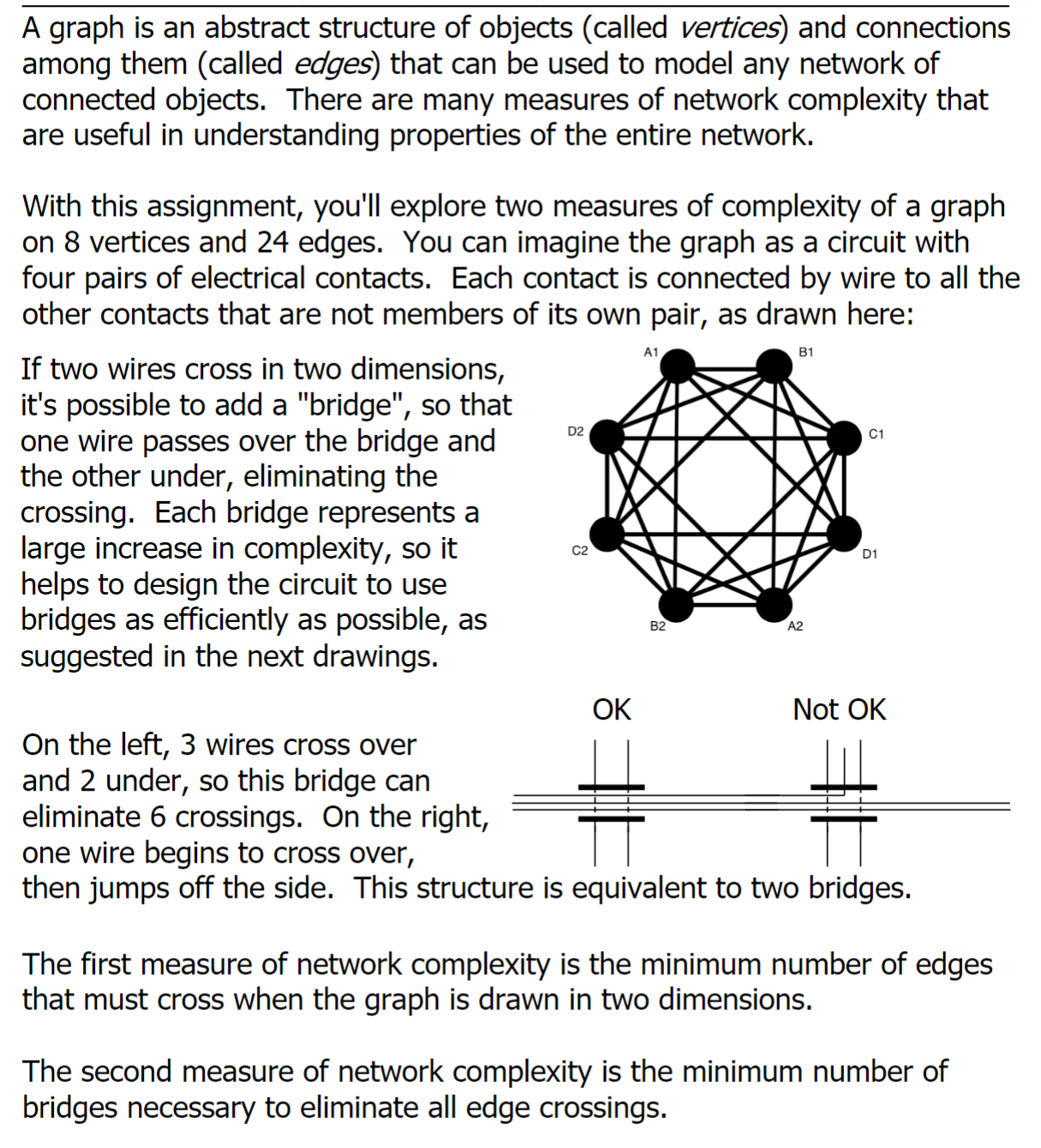
With this assignment, you'll explore two measures of complexity of a graph

on $8$ vertices and $24$ edges. You can imagine the graph as a circuit with

four pairs of electrical contacts. Each contact is connected by wire to all the

other contacts that are not members of its own pair, as drawn here:

If two wires cross in two dimensions,

it's possible to add a "bridge", so that

one wire passes over the bridge and

the other under, eliminating the

crossing. Each bridge represents a

large increase in complexity, so it

helps to design the circuit to use

bridges as efficiently as possible, as

suggested in the next drawings.

On the left, $3$ wires cross over

and $2$ under, so this bridge can

eliminate $6$ crossings. On the right,

one wire begins to cross over,

then jumps off the side. This structure is equivaleril to cwo vriuges.

The first measure of network complexity is the minimum number of edges

that must cross when the graph is drawn in two dimensions.

The second measure of network complexity is the minimum number of

bridges necessary to eliminate all edge crossings. To complete this assignment, prepare two sketches and a written reflection.

a$)$ Make a two$-$dimensional sketch of the graph with as few

edge crossings as you can.

b$)$ Make a second sketch of the graph with as few bridges as necessary

to eliminate all edge crossings in two dimensions.

c$)$ Write a one$-$page reflection on your experience.

Work it out, write it up$.$

I'll assess these papers by the number of crossings in the first sketch and

the number of bridges in the second, the fewer the better. In the reflection,

I'll look for your reasoning as to why you believe you've found the

minumum number of crossings and bridges.

This drawing has $40$ edge crossings.

Contact groups are labeled with

letters, and only different$-$letter

contacts are connected.

You can do better. Edges need not be represented by straight line

segments, for instance. In fact, it's possible to eliminate four crossings

right away by routing the edge joining vertices $A1$ and $C1$ to loop outside of

vertex B$1.$ Make sense?